练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图1，在正方形ABCD中，AB＝2，E是AB边的中点，F是BC边上的一点，对角线AC分别交DE、DF于M、N两点．将△DAE，△DCF折起，使A、C重合于点，构成如图2所示的几何体．

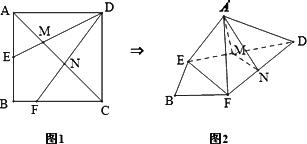
    (Ⅰ)求证：D⊥面EF；

    (Ⅱ)试探究：在图1中，F在什么位置时，能使折起后的几何体中EF∥平面AMN，并给出证明．

    答案：
    解析：

    　　解：(Ⅰ)，2分

    　　又，4分

    　　面．5分

    　　(Ⅱ)当点F为BC的中点时，面．6分

    　　证明如下：当点F为BC的中点时，

    　　在图(1)中，分别是，的中点，

    　　所以，8分

    　　即在图(2)中有．9分

    　　又，，11分

    　　所以面．12分


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

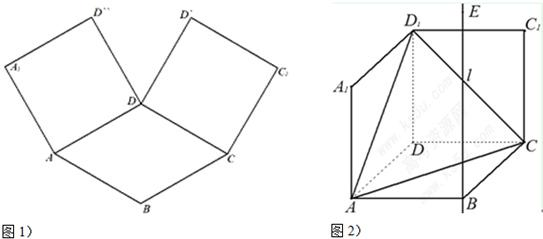
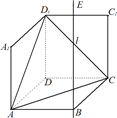    精英家教网如图1，在平面内，ABCD是∠BAD=60°，且AB=a的菱形，ADD′′A1和CD D′C1都是正方形．将两个正方形分别沿AD，CD折起，使D′′与D′重合于点D1．设直线l过点B且垂直于菱形ABCD所在的平面，点E是直线l上的一个动点，且与点D1位于平面ABCD同侧（图2）．
    （Ⅰ） 设二面角E-AC-D1的大小为θ，若
    π
    4
    ≤θ≤
    π
    3
    ，求线段BE长的取值范围；
    （Ⅱ）在线段D1E上存在点P，使平面PA1C1∥平面EAC，求
    D1P
    PE
    与BE之间满足的关系式，并证明：当0＜BE＜a时，恒有
    D1P
    PE
    ＜1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    19、如图1，在边长为12的正方形AA′A′1A1中，BB1∥CC1∥AA1，且AB=3，BC=4，AA′1分别交BB1，CC1于点P、Q，将该正方形沿BB1、CC1折叠，使得A′A′1与AA1重合，构成如图2所示的三棱柱ABC-A1B1C1，请在图2中解决下列问题：
    （1）求证：AB⊥PQ；
    （2）在底边AC上有一点M，满足AM；MC=3：4，求证：BM∥平面APQ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图1，在平面内，ABCD是∠BAD=60°且AB=a的菱形，ADD''A1和CDD'C1都是正方形．将两个正方形分别沿AD，CD折起，使D''与D'重合于点D1．设直线l过点B且垂直于菱形ABCD所在的平面，点E是直线l上的一个动点，且与点D1位于平面ABCD同侧，设BE=t（t＞0）（图2）．
    （1）设二面角E-AC-D1的大小为q，若
    π
    4
    ≤θ≤
    π
    3
    ，求t的取值范围；
    （2）在线段D1E上是否存在点P，使平面PA1C1∥平面EAC，若存在，求出P分
    D1E
    所成的比λ；若不存在，请说明理由．
    精英家教网

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图1-14,在正方形ABCD中，E是BC的中点，F是CD上一点,AE⊥EF,则下列结论正确的是(    )

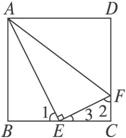
    图1-14

    A.∠BAE=30°         B.CE2=AB·CF       C.CF=CD          D.△ABE∽△AEF

    查看答案和解析>>

    同步练习册答案