
【题目】如图,三棱柱ABC﹣A1B1C1中,侧棱A1A⊥底面ABC,AC=BC,D、E、F分别为棱AB,BC,A1C1的中点. 
(1)证明:EF∥平面A1CD;
(2)证明:平面A1CD⊥平面ABB1A1 .
【答案】
(1)证明:连结DE,
∵D,E分别是AB,BC的中点
∴DE∥AC,DE= ![]() AC,
AC,
∵F为棱A1C1的中点.
∴A1F= ![]() A1C1,
A1C1,
∴A1F∥ ![]() AC,
AC,
即DE∥A1F,DE=A1F,
∴四边形A1DEF为平行四边形,
∴A1D∥EF
又∵EF平面A1CD,A1D平面A1CD,
∴EF∥平面A1CD
(2)证明:∵A1A⊥平面ABC,CD平面ABC,
∴AA1⊥CD,
∵AC=BC,D为AB的中点,
∴AB⊥CD,
∵A1A∩AB=A
∴CD⊥平面ABB1A1
∵CD平面A1CD,
∴平面A1CD⊥平面ABB1A1.
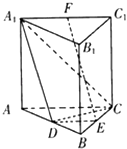
【解析】(1)根据线面平行的判定定理证明EF∥A1D即可证明EF∥平面A1CD;(2)根据面面垂直的判定定理即可证明平面A1CD⊥平面ABB1A1 .
【考点精析】本题主要考查了直线与平面平行的判定和平面与平面垂直的判定的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;一个平面过另一个平面的垂线,则这两个平面垂直才能正确解答此题.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
【题目】函数y=f(x)的定义域为(﹣a,0)∪(0,a)(0<a<1),其图象上任意一点P(x,y)满足x2+y2=1,则给出以下四个命题:①函数y=f(x)一定是偶函数;②函数y=f(x)可能是奇函数;③函数y=f(x)在(0,a)上单调递增④若函数y=f(x)是偶函数,则其值域为(a2 , 1)其中正确的命题个数为( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
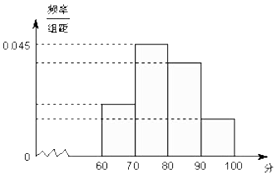
【题目】下面是被严重破坏的频率分布表和频率分布直方图,根据残表和残图,则 p= , q= .
分数段 | 频数 | |
[60,70) | p | |
[70,80) | 90 | |
[80,90) | 60 | |
[90,100] | 20 | q |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和Sn=3n2+8n,{bn}是等差数列,且an=bn+bn+1 . (Ⅰ)求数列{bn}的通项公式;
(Ⅱ)令cn= ![]() ,求数列{cn}的前n项和Tn .
,求数列{cn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方体ABCD﹣A1B1C1D1的棱线长为1,线段B1D1上有两个动点E,F,且EF= ![]() ,则下列结论中错误的是( )
,则下列结论中错误的是( ) 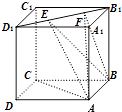
A.AC⊥BE
B.EF∥平面ABCD
C.三棱锥A﹣BEF的体积为定值
D.异面直线AE,BF所成的角为定值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(1)判断f(x)的奇偶性;
(2)用单调性的定义证明f(x)为R上的增函数;
(3)若对任意的t∈R,不等式f(mt2+1)+f(1﹣mt)>0恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=4x+a2x+b,
(1)若f(0)=1,f(﹣1)=﹣ ![]() ,求f(x)的解析式;
,求f(x)的解析式;
(2)由(1)当0≤x≤2时,求函数f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出如下四个命题: ①若“p∨q”为真命题,则p,q均为真命题;
②“若a>b,则2a>2b﹣1”的否命题为“若a≤b,则2a≤2b﹣1”;
③“x∈R,x2+x≥1”的否定是“x0∈R,x ![]() +x0≤1”;
+x0≤1”;
④“x>1”是“x>0”的充分不必要条件.
其中不正确的命题是( )
A.①②
B.②③
C.①③
D.③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com