
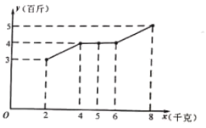
【题目】某基地蔬菜大棚采用水培、无土栽培方式种植各类菠菜.根据统计,该基地的西红种增加量y(百斤)与使用某种液体肥料x(千克)之间对应数据为如图所示的折线图.依据折线图及其提供的数据,是否可用线性回归模型拟合y与x的关系?如果可以,请计算相关系数r并加以说明(精确到0.01),(若![]() ,则线性相关程度很高,可用线性回归模型拟合)
,则线性相关程度很高,可用线性回归模型拟合)
附:相关系数公式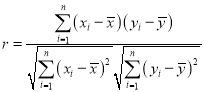 ,参考数据:
,参考数据:![]() ,
,![]() .
.
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中数学 来源: 题型:
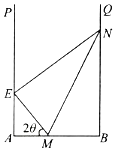
【题目】某地拟在一个U形水面PABQ(∠A=∠B=90°)上修一条堤坝(E在AP上,N在BQ上),围出一个封闭区域EABN,用以种植水生植物.为了美观起见,决定从AB上点M处分别向点E,N拉2条分隔线ME,MN,将所围区域分成3个部分(如图),每部分种植不同的水生植物.已知AB=a,EM=BM,∠MEN=90°,设所拉分隔线总长度为l.
(1)设∠AME=2θ,求用θ表示的l函数表达式,并写出定义域;
(2)求l的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,![]() ,
,![]() ,E为AB的中点将
,E为AB的中点将![]() 沿直线DE折起到
沿直线DE折起到![]() 的位置,使平面
的位置,使平面![]() 平面BCDE.
平面BCDE.
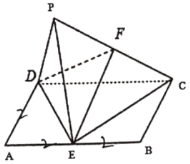
(1)证明:![]() 平面PDE.
平面PDE.
(2)设F为线段PC的中点,求四面体D-PEF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() ,
,![]() 是函数
是函数![]()
![]() 图象上的任意两点,且角
图象上的任意两点,且角![]() 的终边经过点
的终边经过点![]() ,若
,若![]() 时,
时,![]() 的最小值为
的最小值为![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)若方程![]() 在
在![]() 内有两个不同的解,求实数
内有两个不同的解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,在三棱柱![]() 中,
中,![]() 平面
平面![]() 是线段
是线段![]() 上的动点,
上的动点,![]() 是线段
是线段![]() 上的中点.
上的中点.
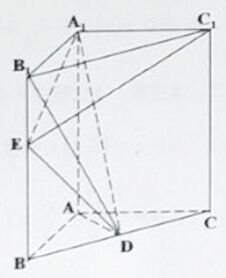
(Ⅰ)证明:![]() ;
;
(Ⅱ)若![]() ,且直线
,且直线![]() 所成角的余弦值为
所成角的余弦值为![]() ,试指出点
,试指出点![]() 在线段
在线段![]() 上的位置,并求三棱锥
上的位置,并求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com