
【题目】如图,在平行四边形ABCD中,![]() ,
,![]() ,E为AB的中点将
,E为AB的中点将![]() 沿直线DE折起到
沿直线DE折起到![]() 的位置,使平面
的位置,使平面![]() 平面BCDE.
平面BCDE.
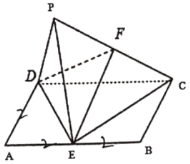
(1)证明:![]() 平面PDE.
平面PDE.
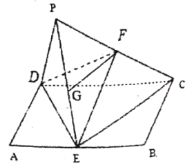
(2)设F为线段PC的中点,求四面体D-PEF的体积.
【答案】(1)见解析;(2)![]()
【解析】
(1)在四边形ABCD中,根据已知角的大小和边的大小关系,可得DE⊥CE,又平面![]() 平面BCDE,根据面面垂直的性质定理可得CE⊥平面PDE;
平面BCDE,根据面面垂直的性质定理可得CE⊥平面PDE;
(2)根据棱锥体积公式可知![]() ,取PE的中点G,可得
,取PE的中点G,可得![]() ,进而
,进而![]() 平面PDE,故FG是三棱锥F-PDE,以F为顶点时的高,分别求出
平面PDE,故FG是三棱锥F-PDE,以F为顶点时的高,分别求出![]() 和FG即可求出四面体D-PEF的体积.
和FG即可求出四面体D-PEF的体积.
(1)因为![]() ,E为AB的中点,则
,E为AB的中点,则![]() .
.
又![]() ,则
,则![]() 为正三角形,所以
为正三角形,所以![]() .
.
因为![]() ,
,![]() ,则
,则![]() .
.
从而![]() ,即
,即![]() .
.
因为平面![]() 平面BCDE,平面
平面BCDE,平面![]() 平面
平面![]() .
.
![]() 平面BCDE,所以
平面BCDE,所以![]() 平面PDE.
平面PDE.
(2)取PE中点G,连结FG.由于E为AB的中点,![]() ,则
,则![]() ,
,
而![]() ,则
,则![]() ,则
,则![]() .
.
因为F为C的中点,则![]() ,所以
,所以![]() 平面PDE .
平面PDE .
在![]() 中,
中,![]() ,
,![]() ,则
,则
![]() ,即
,即![]() ,所以
,所以![]() ,
,
则![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
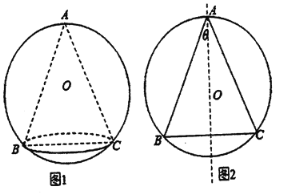
【题目】某艺术品公司欲生产一款迎新春工艺礼品,该礼品是由玻璃球面和该球的内接圆锥组成,圆锥的侧面用于艺术装饰,如图1.为了便于设计,可将该礼品看成是由圆O及其内接等腰三角形![]() 绕底边
绕底边![]() 上的高所在直线
上的高所在直线![]() 旋转
旋转![]() 而成,如图2.已知圆O的半径为
而成,如图2.已知圆O的半径为![]() ,设
,设![]() ,
,![]() ,圆锥的侧面积为
,圆锥的侧面积为![]() (S圆锥的侧面积
(S圆锥的侧面积![]() (R-底面圆半径,I-母线长))
(R-底面圆半径,I-母线长))
(1)求S关于![]() 的函数关系式;
的函数关系式;
(2)为了达到最佳观赏效果,要求圆锥的侧面积S最大.求S取得最大值时腰![]() 的长度
的长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九世纪末:法国学者贝特朗在研究几何概型时提出了“贝特朗悖论”,即“在一个圆内任意选一条弦,这条弦的弦长长于这个圆的内接等边三角形边长的概率是多少?”贝特朗用“随机半径”“随机端点”“随机中点”三个合理的求解方法,但结果都不相同.该悖论的矛头直击概率概念本身,强烈地刺激了概率论基础的严格化.已知“随机端点”的方法如下:设![]() 为圆
为圆![]() 上一个定点,在圆周上随机取一点
上一个定点,在圆周上随机取一点![]() ,连接
,连接![]() ,所得弦长
,所得弦长![]() 大于圆
大于圆![]() 的内接等边三角形边长的概率.则由“随机端点”求法所求得的概率为( )
的内接等边三角形边长的概率.则由“随机端点”求法所求得的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
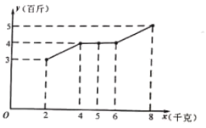
【题目】某基地蔬菜大棚采用水培、无土栽培方式种植各类菠菜.根据统计,该基地的西红种增加量y(百斤)与使用某种液体肥料x(千克)之间对应数据为如图所示的折线图.依据折线图及其提供的数据,是否可用线性回归模型拟合y与x的关系?如果可以,请计算相关系数r并加以说明(精确到0.01),(若![]() ,则线性相关程度很高,可用线性回归模型拟合)
,则线性相关程度很高,可用线性回归模型拟合)
附:相关系数公式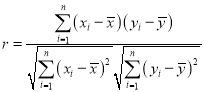 ,参考数据:
,参考数据:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知有限项的、正整数的递增数列![]() ,并满足如下条件:对任意不大于各项总和
,并满足如下条件:对任意不大于各项总和![]() 的正整数
的正整数![]() ,总存在一个子列,使得该子列所有项的和恰好等于
,总存在一个子列,使得该子列所有项的和恰好等于![]() .这里的‘子列’是指由原数列中的一部分项(包括一项、所有项)组成的新数列.
.这里的‘子列’是指由原数列中的一部分项(包括一项、所有项)组成的新数列.
(1)写出![]() ,
,![]() 的值;
的值;
(2)“![]() 成等差数列”的充要条件是“
成等差数列”的充要条件是“![]() 各项总和
各项总和![]() 恰好是其项数、项数平方值的等差中项”.为什么?请说明理由.
恰好是其项数、项数平方值的等差中项”.为什么?请说明理由.
(3)若![]() ,写出“
,写出“![]() 项数最少时,
项数最少时,![]() 中的最大项”的值.
中的最大项”的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
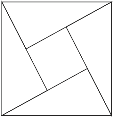
【题目】2002年8月在北京召开的国际数学家大会会标如图所示,它是由4个相同的直角三角形与中间的小正方形拼成的一大正方形,设直角三角形中较小的锐角为![]() ,大正方形的面积是1,小正方形的面积是
,大正方形的面积是1,小正方形的面积是![]() .若
.若![]() ,
,![]() ,则
,则![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,其中
,其中![]() ,若
,若![]() 是
是![]() 的三条边长,则下列结论中正确的是( )
的三条边长,则下列结论中正确的是( )
①存在![]() ,使
,使![]() 、
、![]() 、
、![]() 不能构成一个三角形的三条边
不能构成一个三角形的三条边
②对一切![]() ,都有
,都有![]()
③若![]() 为钝角三角形,则存在
为钝角三角形,则存在![]() ,使
,使![]()
A. ①② B. ①③ C. ②③ D. ①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com