
 £®
£®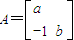 °ÑÖ±Ïßl£ºy=2x-4±ä»»ÎªÖ±Ïßl¡ä£ºy=x-12£¬Çóa£¬bµÄÖµ£®
°ÑÖ±Ïßl£ºy=2x-4±ä»»ÎªÖ±Ïßl¡ä£ºy=x-12£¬Çóa£¬bµÄÖµ£® =1ÉϵĵăPµ½Ö±Ïßl£º3x+4y+18=0µÄ¾àÀëµÄ×îĐ¡Öµ£®
=1ÉϵĵăPµ½Ö±Ïßl£º3x+4y+18=0µÄ¾àÀëµÄ×îĐ¡Öµ£®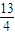 £¬Çóx+y+zµÄ×î´óÖµ£®
£¬Çóx+y+zµÄ×î´óÖµ£®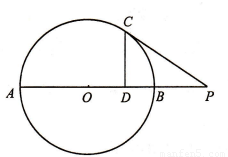
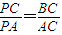 £¬¢ÙÓÖÔÚÖ±½ÇÈư½ÇĐÎABCÖĐ£¬ÓĐ
£¬¢ÙÓÖÔÚÖ±½ÇÈư½ÇĐÎABCÖĐ£¬ÓĐ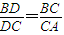 £¬¢Ú£¬µÈÁ¿´ú»»µĂ
£¬¢Ú£¬µÈÁ¿´ú»»µĂ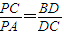 £®
£® £©2+£¨y+1£©2+£¨x+
£©2+£¨y+1£©2+£¨x+ £©2=
£©2= £¬¸ù¾Ư¿ÂÎ÷²»µÈʽ¿ÉµĂµ½[£¨x+
£¬¸ù¾Ư¿ÂÎ÷²»µÈʽ¿ÉµĂµ½[£¨x+ £©+£¨y+1£©+£¨x+
£©+£¨y+1£©+£¨x+ £©]2¡Ü3[£¨x+
£©]2¡Ü3[£¨x+ £©2+£¨y+1£©2+£¨x+
£©2+£¨y+1£©2+£¨x+ £©]=
£©]=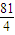 £¬´Ó¶øÇó³öx+y+zµÄ×îĐ¡Öµ£®
£¬´Ó¶øÇó³öx+y+zµÄ×îĐ¡Öµ£®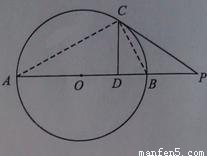 ½â£ºA£®Ö¤Ă÷£ºÁ¬½ÓBC¡¢AC£¬
½â£ºA£®Ö¤Ă÷£ºÁ¬½ÓBC¡¢AC£¬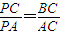 £¬¢Ù
£¬¢Ù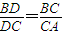 £¬¢Ú
£¬¢Ú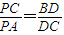 £®
£®
 =
= £¬Ëù̉ÔM'µÄ×ø±êΪ£¨2a£¬-2£©£»
£¬Ëù̉ÔM'µÄ×ø±êΪ£¨2a£¬-2£©£»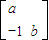
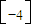 =
=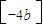 £¬Ëù̉ÔN'µÄ×ø±êΪ£¨0£¬-4b£©£»
£¬Ëù̉ÔN'µÄ×ø±êΪ£¨0£¬-4b£©£»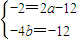
 =
=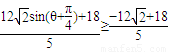
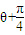 £©=-1ʱ£¬µÈºÅ³ÉÁ¢£¬
£©=-1ʱ£¬µÈºÅ³ÉÁ¢£¬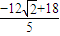 £®
£® £©2+£¨y+1£©2+£¨z+
£©2+£¨y+1£©2+£¨z+ £©2=
£©2=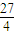
 £©+£¨y+1£©+£¨z+
£©+£¨y+1£©+£¨z+ £©]2¡Ü3[£¨x+
£©]2¡Ü3[£¨x+ £©2+£¨y+1£©2+£¨z+
£©2+£¨y+1£©2+£¨z+ £©2]=
£©2]=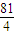
 £¬µ±Ç̉½öµ±£ºx+
£¬µ±Ç̉½öµ±£ºx+ =y+1=z+
=y+1=z+ ʱȡµÈºÅ£¬
ʱȡµÈºÅ£¬ £®
£®

 ÔĶÁ¿́³µÏµÁĐ´đ°¸
ÔĶÁ¿́³µÏµÁĐ´đ°¸
| Ä꼶 | ¸ßÖĐ¿Î³̀ | Ä꼶 | ³ơÖĐ¿Î³̀ |
| ¸ß̉» | ¸ß̉»Ăâ·Ñ¿Î³̀ÍƼö£¡ | ³ở» | ³ở»Ăâ·Ñ¿Î³̀ÍƼö£¡ |
| ¸ß¶₫ | ¸ß¶₫Ăâ·Ñ¿Î³̀ÍƼö£¡ | ³ơ¶₫ | ³ơ¶₫Ăâ·Ñ¿Î³̀ÍƼö£¡ |
| ¸ßÈư | ¸ßÈưĂâ·Ñ¿Î³̀ÍƼö£¡ | ³ơÈư | ³ơÈưĂâ·Ñ¿Î³̀ÍƼö£¡ |
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º
|
| a |
|
|
| x2 |
| 4 |
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º ̀âĐÍ£º
 £¨2012•½ËƠ¶₫Ä££©Ñ¡×ö̀â
£¨2012•½ËƠ¶₫Ä££©Ñ¡×ö̀â| PC |
| PA |
| BD |
| DC |
|
| x2 |
| 16 |
| y2 |
| 9 |
| 13 |
| 4 |
²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º2010Äê½ËƠÊ¡ÑïÖƯÖĐѧ¸ßÈưµÚËÄ´ÎÄ£Ä⿼ÊÔÊưѧÊỒâ ̀âĐÍ£º½â´đ̀â
[Ñ¡×ö̀â]
A£®Ñ¡Đ̃4¡ª1£º¼¸ºÎÖ¤Ă÷Ñ¡½²
Èçͼ£¬ÉèABΪ¡ÑOµÄÈÎ̉»̀ơ²»ÓëÖ±Ïßl´¹Ö±µÄÖ±¾¶£¬PÊÇ¡ÑOÓëlµÄ¹«¹²µă£¬AC¡Íl£¬BD¡Íl£¬´¹×ă·Ö±đΪC£¬D£¬Ç̉PC=PD£¬ÇóÖ¤£º
£¨1£©lÊÇ¡ÑOµÄÇĐÏߣ»
£¨2£©PBƽ·Ö¡ÏABD£®
|
 ¶ÔÓ¦µÄ±ä»»½«µă
¶ÔÓ¦µÄ±ä»»½«µă Óë
Óë ·Ö±đ±ä»»³Éµă
·Ö±đ±ä»»³Éµă Óë
Óë £®Çó¾ØƠó
£®Çó¾ØƠó £»
£» µÄ×î´óÖµ£®
µÄ×î´óÖµ£®²é¿´´đ°¸ºÍ½âÎö>>
¿ÆÄ¿£º¸ßÖĐÊưѧ À´Ô´£º2010Äê½ËƠÊ¡¸ßÈưµÚËÄ´ÎÄ£Ä⿼ÊÔÊưѧÊỒâ ̀âĐÍ£º½â´đ̀â
[Ñ¡×ö̀â]
A£®Ñ¡Đ̃4¡ª1£º¼¸ºÎÖ¤Ă÷Ñ¡½²
Èçͼ£¬ÉèABΪ¡ÑOµÄÈÎ̉»̀ơ²»ÓëÖ±Ïßl´¹Ö±µÄÖ±¾¶£¬PÊÇ¡ÑOÓëlµÄ¹«¹²µă£¬AC¡Íl£¬BD¡Íl£¬´¹×ă·Ö±đΪC£¬D£¬Ç̉PC=PD£¬ÇóÖ¤£º
£¨1£©lÊÇ¡ÑOµÄÇĐÏߣ»
£¨2£©PBƽ·Ö¡ÏABD£®

B£®Ñ¡Đ̃4¡ª2£º¾ØƠóÓë±ä»»
¶₫½×¾ØƠó ¶ÔÓ¦µÄ±ä»»½«µă
¶ÔÓ¦µÄ±ä»»½«µă Óë
Óë ·Ö±đ±ä»»³Éµă
·Ö±đ±ä»»³Éµă Óë
Óë £®Çó¾ØƠó
£®Çó¾ØƠó £»
£»
C£®Ñ¡Đ̃4¡ª4£º×ø±êϵÓë²ÎÊư·½³̀
ÈôÁ½̀ơÇúÏߵļ«×ø±ê·½³̀·Ö±đΪ=lÓë=2cos(¦È+)£¬ËüĂÇÏཻÓÚA£¬BÁ½µă£¬ÇóÏß
¶ÎABµÄ³¤£®
D£®Ñ¡Đ̃4¡ª5£º²»µÈʽѡ½²
Çóº¯Êư µÄ×î´óÖµ£®
µÄ×î´óÖµ£®
²é¿´´đ°¸ºÍ½âÎö>>
¹ú¼ÊÑ§Đ£ÓÅÑ¡ - Á·Ï°²áÁбí - ÊỒâÁбí
º₫±±Ê¡»¥ÁªÍøÎ¥·¨ºÍ²»Á¼ĐÅÏ¢¾Ù±¨Æ½̀¨ | ÍøÉÏÓĐº¦ĐÅÏ¢¾Ù±¨×¨Çø | µçĐÅƠ©Æ¾Ù±¨×¨Çø | ÉæÀúÊ·ĐéÎ̃Ö÷̉åÓĐº¦ĐÅÏ¢¾Ù±¨×¨Çø | ÉæÆóÇÖȨ¾Ù±¨×¨Çø
Î¥·¨ºÍ²»Á¼ĐÅÏ¢¾Ù±¨µç»°£º027-86699610 ¾Ù±¨ÓÊÏ䣺58377363@163.com