
 。
。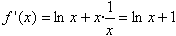
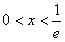
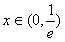 时,f(x)为减函数
时,f(x)为减函数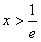
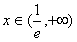 时,f(x)为增函数
时,f(x)为增函数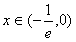 时,f(x)为减函数,
时,f(x)为减函数,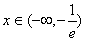 时,f(x)为增函数
时,f(x)为增函数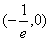 和
和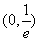
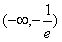 和
和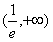 。
。 ,结合f(x)的图象变化,由(2)知,
,结合f(x)的图象变化,由(2)知,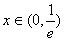 时f(x)由0递减到
时f(x)由0递减到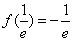
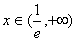 时f(x)由
时f(x)由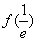 递增到+∞
递增到+∞ 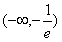 时f(x)由-∞递增到
时f(x)由-∞递增到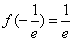
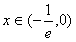 时f(x)由
时f(x)由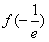 递减到0
递减到0 恰有3个不同的根,
恰有3个不同的根,  的图象应有3个不同的交点,
的图象应有3个不同的交点, 或
或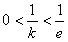


 每课必练系列答案
每课必练系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:

 (理)已知函数f(x)=
(理)已知函数f(x)=| ln(2-x2) |
| |x+2|-2 |
| AB |
| AD |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1-xp |
| 1+λxp |
| 1 |
| p |
| 1 |
| n |
| n |
 |
| i=1 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(09年崇文区二模文)(14分)
已知直线![]() ,抛物线
,抛物线![]() ,定点M(1,1)。
,定点M(1,1)。
(I)当直线![]() 经过抛物线焦点F时,求点M关于直线
经过抛物线焦点F时,求点M关于直线![]() 的对称点N的坐标,并判断点N 是否在抛物线C上;
的对称点N的坐标,并判断点N 是否在抛物线C上;
(II)当![]() 变化且直线
变化且直线![]() 与抛物线C有公共点时,设点P(a,1)关于直线
与抛物线C有公共点时,设点P(a,1)关于直线![]() 的对称点为Q(x0,y0),求x0关于k的函数关系式
的对称点为Q(x0,y0),求x0关于k的函数关系式![]() ;当
;当![]() 且P与M重合时,求
且P与M重合时,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
已知直线![]() ,抛物线
,抛物线![]() ,
,
定点M(1,1)。
(I)当直线![]() 经过抛物线焦点F时,求点M关于直线
经过抛物线焦点F时,求点M关于直线![]() 的对称点N的坐标,并判断点N 是否在抛物线C上;
的对称点N的坐标,并判断点N 是否在抛物线C上;
(II)当![]() 变化且直线
变化且直线![]() 与抛物线C有公共点时,设点P(a,1)关于直线
与抛物线C有公共点时,设点P(a,1)关于直线![]() 的对称点为Q(x0,y0),求x0关于k的函数关系式
的对称点为Q(x0,y0),求x0关于k的函数关系式![]() ;若P与M重合时,求
;若P与M重合时,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com