
【题目】2018年12月28日,成雅铁路开通运营,使川西多个市县进入动车时代,融入全国高铁网,这对推动沿线经济社会协调健康发展具有重要意义.在试运行期间,铁道部门计划在成都和雅安两城之间开通高速列车,假设每天7:00-8:00,8:00-9:00两个时间段内各发一趟列车由雅安到成都(两车发车情况互不影响),雅安发车时间及其概率如下表所示:
第一趟列车 | 第二趟列车 | |||||
发车时间 | 7:10 | 7:30 | 7:50 | 8:10 | 8:30 | 8:50 |
概率 | 0.2 | 0.3 | 0.5 | 0.2 | 0.3 | 0.5 |
若小王、小李二人打算乘动车从雅安到成都游玩,假设他们到达雅安火车站候车的时间分别是周六7:00和7:20(只考虑候车时间,不考虑其它因素).
(1)求小王候车10分钟且小李候车30分钟的概率;
(2)设小李候车所需时间为随机变量![]() ,求
,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
科目:高中数学 来源: 题型:
【题目】“工资条里显红利,个税新政入民心”.随着2019年新年钟声的敲响,我国自1980年以来,力度最大的一次个人所得税(简称个税)改革迎来了全面实施的阶段.某![]() 从业者为了解自己在个税新政下能享受多少税收红利,绘制了他在26岁-35岁(2009年-2018年)之间各年的月平均收入
从业者为了解自己在个税新政下能享受多少税收红利,绘制了他在26岁-35岁(2009年-2018年)之间各年的月平均收入![]() (单位:千元)的散点图:(注:年龄代码1-10分别对应年龄26-35岁)
(单位:千元)的散点图:(注:年龄代码1-10分别对应年龄26-35岁)
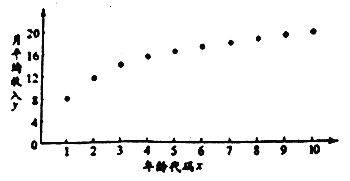
(1)由散点图知,可用回归模型![]() 拟合
拟合![]() 与
与![]() 的关系,试根据有关数据建立
的关系,试根据有关数据建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(2)如果该![]() 从业者在个税新政下的专项附加扣除为3000元/月,试利用(1)的结果,将月平均收入视为月收入,根据新旧个税政策,估计他36岁时每个月少缴纳的个人所得税.
从业者在个税新政下的专项附加扣除为3000元/月,试利用(1)的结果,将月平均收入视为月收入,根据新旧个税政策,估计他36岁时每个月少缴纳的个人所得税.
附注:①参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,其中
,其中![]() :取
:取![]() ,
,![]() .
.
②参考公式:回归方程![]() 中斜率和截距的最小二乘估计分别为
中斜率和截距的最小二乘估计分别为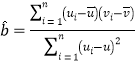 ,
,![]() .
.
③新旧个税政策下每月应纳税所得额(含税)计算方法及税率表如下:
旧个税税率表(个税起征点3500元) | 新个税税率表(个税起征点5000元) | |||
缴税 级数 | 每月应纳税所得额(含税) | 税率 | 每月应纳税所得额(含税) | 税率 |
1 | 不超过1500元的都分 | 3 | 不超过3000元的都分 | 3 |
2 | 超过1500元至4500元的部分 | 10 | 超过3000元至12000元的部分 | 10 |
3 | 超过4500元至9000元的部分 | 20 | 超过12000元至25000元的部分 | 20 |
4 | 超过9000元至35000元的部分 | 25 | 超过25000元至35000元的部分 | 25 |
5 | 超过35000元至55000元的部分 | 30 | 超过35000元至55000元的部分 | 30 |
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如表是某位同学连续5次周考的数学、物理的成绩,结果如下:
周次 | 1 | 2 | 3 | 4 | 5 |
数学( | 79 | 81 | 83 | 85 | 87 |
物理( | 77 | 79 | 79 | 82 | 83 |
参考公式: ,
,![]() ,
,![]() 表示样本均值.
表示样本均值.
(1)求该生5次月考数学成绩的平均分和物理成绩的方差;
(2)一般来说,学生的数学成绩与物理成绩有较强的线性相关关系,根据上表提供的数据,求两个变量![]() 的线性回归方程.
的线性回归方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查某省高三男生身高情况,现从某校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于157.5cm和187.5cm之间,将测量结果按如下方式分成6组:第一组![]() ,第二组
,第二组![]() ,…,第六组
,…,第六组![]() ,下图是按照上述分组方法得到的频率分布直方图.
,下图是按照上述分组方法得到的频率分布直方图.
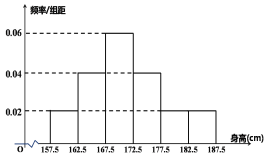
(1)求该学校高三年级男生的平均身高;
(2)利用分层抽样的方式从这50名男生中抽出20人,求抽出的这20人中,身高在177.5cm以上(含177.5cm)的人数;
(3)从根据(2)选出的身高在177.5cm以上(含177.5cm)的男生中任意抽取2人,求此二人来自于不同组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三条直线![]() :
:![]() (
(![]() ),
),![]() :
:![]() ,
,![]() :
:![]() ,若
,若![]() 与
与![]() 的距离是
的距离是![]() .
.
(1)求a的值:
(2)能否找到一点P,使得点P同时满足下列三个条件:①P是第一象限的点;②点P到![]() 的距离是点P到
的距离是点P到![]() 的距离的
的距离的![]() ;③点P到
;③点P到![]() 的距离与点P到
的距离与点P到![]() 的距离之比是
的距离之比是![]() ,若能,求出点P的坐标,若不能,请说明理由.
,若能,求出点P的坐标,若不能,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正方体![]() 中,如果动点
中,如果动点![]() 在线段
在线段![]() 上,动点
上,动点![]() 在正方体
在正方体![]() 的四条边上,那么,对于任何一条直线
的四条边上,那么,对于任何一条直线![]() ,在平面
,在平面![]() 上,总存在相应的一条直线,使得该直线与直线
上,总存在相应的一条直线,使得该直线与直线![]() ( )
( )
A.平行B.异面C.相交D.垂直
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P—ABC中,PA=3,PB=PC=![]() ,AB=AC=2,BC=
,AB=AC=2,BC=![]() .
.
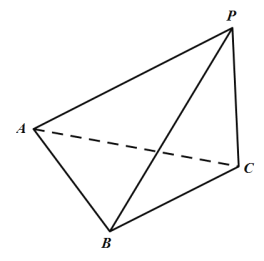
(1)求二面角B—AP—C大小的余弦值;
(2)求点P到底面ABC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的方程为
的方程为![]() ,
,![]() ,
,![]() 为椭圆
为椭圆![]() 的左右顶点,
的左右顶点,![]() 为椭圆
为椭圆![]() 上不同于
上不同于![]() .
.![]() 的动点,直线
的动点,直线![]() 与直线
与直线![]() ,
,![]() 分别交于
分别交于![]() ,
,![]() 两点,若
两点,若![]() ,则过
,则过![]() ,
,![]() ,
,![]() 三点的圆必过
三点的圆必过![]() 轴上不同于点
轴上不同于点![]() 的定点,其坐标为__________.
的定点,其坐标为__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com