【答案】
分析:解法一(I)由AD⊥面DEFG和直角梯形EFGD可知,AD、DE、DG两两垂直,建立如图的坐标系,写出要用的点的坐标,要证明的四点共面中的两条线平行,根据共面的判定得到结论.
(II)要求两个平面的夹角,只要写出两个平面的法向量,根据法向量所成的角来解题,本题所给的两个平面,有一个法向量可以直接由题意得到,而另一个需要根据向量垂直做出结果.
(III)设DG的中点为M,连接AM、FM,则V
多面体ABC-DEFG=V
三棱柱ADM-BEF+V
三棱柱ABC-MFG,把一个不规则几何体的体积转化成两个三棱柱的体积之和,做出三棱柱的体积相加即可.
解法二(I)设DG的中点为M,连接AM、FM,则由已知条件易证四边形DEFM是平行四边形,根据一组对边平行且相等,即AC∥MG,且AC=MG,即四边形ACGM是平行四边形,得到结论.
(II)根据做两个平面所成的角的方法,先做出角,在证明角,最后求出角,这样根据在平面ADGC中,过M作MN⊥GC,垂足为N,连接NF,则∠MNF是所求二面角的平面角,后面求出角的大小即可.
(III)连接AM、FM,则V
多面体ABC-DEFG=V
三棱柱ADM-BEF+V
三棱柱ABC-MFG,把一个不规则几何体的体积转化成两个三棱柱的体积之和,做出三棱柱的体积相加即可.
解答:解法一 向量法
由 AD⊥面DEFG和直角梯形EFGD可知,AD、DE、DG两两垂直,建立如图的坐标系,则A(0,0,2),B(2,0,2),C(0,1,2),E(2,0,0),G(0,2,0),F(2,1,0)
(1)
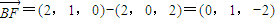

∴

,即四边形BCGF是平行四边形.
故四点B、C、F、G共面.…(4分)

(2)

,
设平面BCGF的法向量为

,
则

,
令y=2,则

,
而平面ADGC的法向量

∴

=

故面ADGC与面BCGF所组成的二面角余弦值为

.…(8分)
(3)设DG的中点为M,连接AM、FM,则V
多面体ABC-DEFG=V
三棱柱ADM-BEF+V
三棱柱ABC-MFG=DE×S
△ADM+AD×S
△MFG=

=4.…(12分)
解法二 (1)设DG的中点为M,连接AM、FM,则由已知条件易证四边形DEFM是平行四边形,所以MF∥DE,且MF=DE
又∵AB∥DE,且AB=DE∴MF∥AB,且MF=AB
∴四边形ABMF是平行四边形,即BF∥AM,且BF=AM
又∵M为DG的中点,DG=2,AC=1,面ABC∥面DEFG
∴AC∥MG,且AC=MG,即四边形ACGM是平行四边形
∴GC∥AM,且GC=AM
故GC∥BF,且GC=BF,
即四点B、C、F、G共面…(4分)

(2)∵四边形EFGD是直角梯形,AD⊥面DEFG
∴DE⊥DG,DE⊥AD,即DE⊥面ADGC,
∵MF∥DE,且MF=DE,∴MF⊥面ADGC
在平面ADGC中,过M作MN⊥GC,垂足为N,连接NF,则
显然∠MNF是所求二面角的平面角.
∵在四边形ADGC中,AD⊥AC,AD⊥DG,AC=DM=MG=1
∴

,∴cos∠DGC=

=

=

∴

,∴MN=MG•sin∠DGC=

在直角三角形MNF中,MF=2,MN=

∴tan∠MNF=

=

=

,cos∠MNF=

故面ADGC与面BCGF所组成的二面角余弦值为

…(8分)

(3)V
多面体ABC-DEFG=V
三棱柱ADM-BEF+V
三棱柱ABC-MFG=DE×S
△ADM+AD×S
△MFG=

=4.…(12分)
点评:本题以不规则几何体为载体,考查空间线面关系的判断与证明,空间几何量的计算,准确把握立体几何的最新发展趋势:由正方体、正四棱柱等规则几何体的考查向不规则几何体过渡,但仍坚持向量法与公理化法的“双轨”处理模式,在复习备考时应引起高度注意.


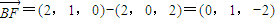

 ,即四边形BCGF是平行四边形.
,即四边形BCGF是平行四边形.
 ,
, ,
, ,
, ,
,
 =
=
 .…(8分)
.…(8分) =4.…(12分)
=4.…(12分)
 ,∴cos∠DGC=
,∴cos∠DGC= =
= =
=
 ,∴MN=MG•sin∠DGC=
,∴MN=MG•sin∠DGC=

 =
= =
= ,cos∠MNF=
,cos∠MNF=
 …(8分)
…(8分)
 =4.…(12分)
=4.…(12分)

 如图,在空间中的直角三角形ABC与直角梯形EFGD中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB∥DE,AC∥DG.且AB=AD=DE=DG=2,AC=EF=1.
如图,在空间中的直角三角形ABC与直角梯形EFGD中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB∥DE,AC∥DG.且AB=AD=DE=DG=2,AC=EF=1.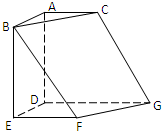 如图,在空间中的直角三角形ABC与直角梯形EFGD中,平面ABC∥平面DEFG,AD⊥平面DEFG,AC∥DG.且AB=AD=DE=DG=2,AC=EF=1.
如图,在空间中的直角三角形ABC与直角梯形EFGD中,平面ABC∥平面DEFG,AD⊥平面DEFG,AC∥DG.且AB=AD=DE=DG=2,AC=EF=1.