
分析 (Ⅰ)由2c=2$\sqrt{3}$,c=$\sqrt{3}$,将$(\frac{{\sqrt{3}}}{2}\;,\;1)$代入$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{a}^{2}-3}=1$,即可求得a和b的值,求得椭圆方程和抛物线E的标准方程;
(Ⅱ)由题意求得直线l1、l2的方程,将直线l1、l2代入代入抛物线方程,利用韦达定理,表示出|AF|•|FB|+|FG|•|HF|=|x1+1|•|x2+1|+|x3+1|•|x4+1|,由基本不等式性质可知$\frac{4}{k^2}=4{k^2}$,即k=±1时,|AF|•|FB|+|FG|•|HF|的最小值为16.
解答 解:(Ⅰ)设椭圆C的标准方程为$\frac{y^2}{a^2}+\frac{x^2}{b^2}=1(a>b>0)$,焦距为2c,
则由题意得$c=\sqrt{3}\;,\;{a^2}=4$,
∴椭圆方程为$\frac{y^2}{4}+{x^2}=1$,抛物线方程为y2=4x.…4分
(Ⅱ)设l1的方程为:y=k(x-1),l2的方程为:$y=-\frac{1}{k}(x-1)$,
设A(x1,y1),B(x2,y2),C(x3,y3),H(x4,y4).
由$\left\{\begin{array}{l}y=k(x-1)\\{y^2}=4x\end{array}\right.$消去y得:k2x2-(2k2+4)x+k2=0,
∴$△=4{k^4}+16{k^2}+16-4{k^4}>0\;,\;{x_1}+{x_2}=2+\frac{4}{k^2}\;,\;{x_1}{x_2}=1$,
同理${x_3}+{x_4}=4{k^2}+2\;,\;{x_3}{x_4}=1$.…6分
∴|AF|•|FB|+|FG|•|HF|=|x1+1|•|x2+1|+|x3+1|•|x4+1|,…8分
=$({x_1}{x_2}+{x_1}+{x_2}+1)+({x_3}{x_4}+{x_3}+{x_4}+1)=8+\frac{4}{k^2}+4{k^2}$,
$≥8+2\sqrt{\frac{4}{k^2}•4{k^2}}=16$,
当且仅当$\frac{4}{k^2}=4{k^2}$,
即k=±1时,|AF|•|FB|+|FG|•|HF|的最小值为16.…12分.
点评 本题考查椭圆及抛物线的标准方程,考查直线与抛物线的位置关系,考查韦达定理,弦长公式及基本不等式的综合运用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\{\left.x\right|-1<x<-\frac{1}{2}或2<x<3\}$ | B. | {x|2<x<3} | ||
| C. | {x|x<2或x>3} | D. | $\{\left.x\right|-\frac{1}{2}<x<2\}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{4}+\frac{y^2}{3}=1$ | B. | $\frac{x^2}{8}+\frac{y^2}{6}=1$ | C. | $\frac{x^2}{2}+{y^2}=1$ | D. | $\frac{x^2}{4}+{y^2}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 小明 | 5 | 7 | 6 | 8 |
| 电脑 | 6 | 9 | 5 | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
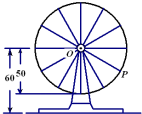 如图,摩天轮的半径为50m,点O距地面的高度为60m,摩天轮做匀速转动,每3min转一圈,摩天轮上点P的起始位置在最低点处.
如图,摩天轮的半径为50m,点O距地面的高度为60m,摩天轮做匀速转动,每3min转一圈,摩天轮上点P的起始位置在最低点处.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com