
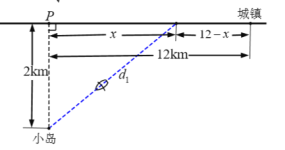
ЁОЬтФПЁПШчЭМЫљЪОЃЌвЛзљаЁЕКОрРыКЃАЖЯпЩЯзюНќЕФPЕуЕФОрРыЪЧ2kmЃЌДгPЕубиКЃАЖе§ЖЋ12kmДІгавЛИіГЧеђ.МйЩшвЛИіШЫМнЪЛЕФаЁДЌЕФЦНОљЫйЖШЮЊ![]() ЃЌВНааЕФЫйЖШЮЊ
ЃЌВНааЕФЫйЖШЮЊ![]() ЃЌЪБМфtЃЈЕЅЮЛЃКhЃЉБэЪОЫћДгаЁЕКЕНГЧеђЕФЪБМфЃЌxЃЈЕЅЮЛЃКkmЃЉБэЪОДЫШЫНЋДЌЭЃдкКЃАЖДІОрPЕуЕФОрРы.Щш
ЃЌЪБМфtЃЈЕЅЮЛЃКhЃЉБэЪОЫћДгаЁЕКЕНГЧеђЕФЪБМфЃЌxЃЈЕЅЮЛЃКkmЃЉБэЪОДЫШЫНЋДЌЭЃдкКЃАЖДІОрPЕуЕФОрРы.Щш![]()
![]() ЃЌдђЃЈ ЃЉ
ЃЌдђЃЈ ЃЉ
A.КЏЪ§![]() ЮЊМѕКЏЪ§B.
ЮЊМѕКЏЪ§B.![]()
C.ЕБ![]() ЪБЃЌДЫШЫДгаЁЕКЕНГЧеђЛЈЗбЕФЪБМфзюЩйD.ЕБ
ЪБЃЌДЫШЫДгаЁЕКЕНГЧеђЛЈЗбЕФЪБМфзюЩйD.ЕБ![]() ЪБЃЌДЫШЫДгаЁЕКЕНГЧеђЛЈЗбЕФЪБМфВЛГЌЙ§3h
ЪБЃЌДЫШЫДгаЁЕКЕНГЧеђЛЈЗбЕФЪБМфВЛГЌЙ§3h
ЁОД№АИЁПAC
ЁОНтЮіЁП
ЯШЧѓГі![]() ЕФЙиЯЕЃЌЕУ
ЕФЙиЯЕЃЌЕУ![]() ЃЌХаЖЯЕЅЕїадЃЛ
ЃЌХаЖЯЕЅЕїадЃЛ
СаГіЪБМф![]() Йигк
Йигк![]() ЕФКЏЪ§ЃЌдйзЊЛЏЮЊ
ЕФКЏЪ§ЃЌдйзЊЛЏЮЊ![]() ЕФЪНзгЃЌПЩХаЖЯBЃЛ
ЕФЪНзгЃЌПЩХаЖЯBЃЛ
РћгУ![]() гы
гы![]() ЕФЙиЯЕЃЌАб
ЕФЙиЯЕЃЌАб![]() БэЪОЮЊ
БэЪОЮЊ![]() ЕФКЏЪ§ЃЌПЩЧѓзюаЁжЕЃЛ
ЕФКЏЪ§ЃЌПЩЧѓзюаЁжЕЃЛ
зїВю![]() ПЩаФБШНЯ
ПЩаФБШНЯ![]() гы3ЕФДѓаЁЃЎ
гы3ЕФДѓаЁЃЎ
A.Ёп![]()
![]() ЃЌЁр
ЃЌЁр![]() ЃЌ
ЃЌ
гЩЬтвт![]() ЃЌ
ЃЌ![]() дк
дк![]() ЩЯЪЧМѕКЏЪ§ЃЌAе§ШЗЃЎ
ЩЯЪЧМѕКЏЪ§ЃЌAе§ШЗЃЎ
B.![]()
![]() ЃЌећРэЕУ
ЃЌећРэЕУ![]() ЃЌBДэЮѓЃЛ
ЃЌBДэЮѓЃЛ
C.гЩAЁЂBЕУ![]() ЃЌ
ЃЌ![]() МД
МД![]() ЪБШЁЕШКХЃЌ
ЪБШЁЕШКХЃЌ
гЩ![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌCе§ШЗЃЛ
ЃЌCе§ШЗЃЛ
D.![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌDДэЃЎ
ЃЌDДэЃЎ
ЙЪбЁЃКAC.


 УћаЃЭЈаажЄгааЇзївЕЯЕСаД№АИ
УћаЃЭЈаажЄгааЇзївЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌЧњЯпCЕФВЮЪ§ЗНГЬЮЊ![]() ЃЌЃЈІШЮЊВЮЪ§ЃЉЃЌвддЕуЮЊМЋЕуЃЌxжсЗЧИКАыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЎ
ЃЌЃЈІШЮЊВЮЪ§ЃЉЃЌвддЕуЮЊМЋЕуЃЌxжсЗЧИКАыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЎ
ЃЈ1ЃЉЧѓЧњЯпCЕФМЋзјБъЗНГЬЃЛ
ЃЈ2ЃЉдкЦНУцжБНЧзјБъЯЕxOyжаЃЌAЃЈЉ2ЃЌ0ЃЉЃЌBЃЈ0ЃЌЉ2ЃЉЃЌMЪЧЧњЯпCЩЯШЮвтвЛЕуЃЌЧѓЁїABMУцЛ§ЕФзюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшAЃЌBСНЕуЕФзјБъЗжБ№ЮЊЃЈЉ1ЃЌ0ЃЉЃЌЃЈ1ЃЌ0ЃЉ.ЬѕМўМзЃКAЁЂBЁЂCШ§ЕуЙЙГЩвдЁЯCЮЊЖлНЧЕФШ§НЧаЮЃЛЬѕМўввЃКЕуCЕФзјБъЪЧЗНГЬx2+2y2=1ЃЈyЁй0ЃЉЕФНтЃЌдђМзЪЧввЕФЃЈЁЁЁЁЃЉ
A.ГфЗжВЛБивЊЬѕМўB.БивЊВЛГфЗжЬѕМў
C.ГфвЊЬѕМўD.МШВЛГфЗжгжВЛБивЊЬѕМў
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊСЫНтФГжабЇбЇЩњЖдЁЖжаЛЊШЫУёЙВКЭЙњНЛЭЈАВШЋЗЈЁЗЕФСЫНтЧщПіЃЌЕїВщВПУХдкИУаЃНјааСЫвЛДЮЮЪОэЕїВщЃЈЙВ12ЕРЬтЃЉЃЌДгИУаЃбЇЩњжаЫцЛњГщШЁ40ШЫЃЌЭГМЦСЫУПШЫД№ЖдЕФЬтЪ§ЃЌНЋЭГМЦНсЙћЗжГЩ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() СљзщЃЌЕУЕНШчЯТЦЕТЪЗжВМжБЗНЭМ.
СљзщЃЌЕУЕНШчЯТЦЕТЪЗжВМжБЗНЭМ.
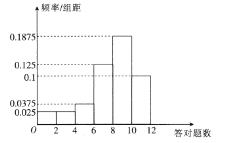
ЃЈ1ЃЉШєД№ЖдвЛЬтЕУ10ЗжЃЌЮДД№ЖдВЛЕУЗжЃЌЙРМЦет40ШЫЕФГЩМЈЕФЦНОљЗжЃЈЭЌвЛзщжаЕФЪ§ОнгУИУзщЧјМфЕФжаЕужЕзїДњБэЃЉЃЛ
ЃЈ2ЃЉШєДгД№ЖдЬтЪ§дк![]() ФкЕФбЇЩњжаЫцЛњГщШЁ2ШЫЃЌЧѓЧЁга1ШЫД№ЖдЬтЪ§дк
ФкЕФбЇЩњжаЫцЛњГщШЁ2ШЫЃЌЧѓЧЁга1ШЫД№ЖдЬтЪ§дк![]() ФкЕФИХТЪ.
ФкЕФИХТЪ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкжБНЧзјБъЯЕ![]() жаЃЌдВ
жаЃЌдВ![]() ЕФЦеЭЈЗНГЬЮЊ
ЕФЦеЭЈЗНГЬЮЊ![]() ЃЎдквдзјБъдЕуЮЊМЋЕуЃЌ
ЃЎдквдзјБъдЕуЮЊМЋЕуЃЌ![]() жсе§АыжсЮЊМЋжсЕФМЋзјБъЯЕжаЃЌжБЯп
жсе§АыжсЮЊМЋжсЕФМЋзјБъЯЕжаЃЌжБЯп![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉаДГідВ![]() ЕФВЮЪ§ЗНГЬКЭжБЯп
ЕФВЮЪ§ЗНГЬКЭжБЯп![]() ЕФжБНЧзјБъЗНГЬЃЛ
ЕФжБНЧзјБъЗНГЬЃЛ
ЃЈ2ЃЉЩшЕу![]() дк
дк![]() ЩЯЃЌЕуQдк
ЩЯЃЌЕуQдк![]() ЩЯЃЌЧѓ
ЩЯЃЌЧѓ![]() ЕФзюаЁжЕМАДЫЪБЕу
ЕФзюаЁжЕМАДЫЪБЕу![]() ЕФжБНЧзјБъЃЎ
ЕФжБНЧзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЩшжааФдкдЕуOЃЌНЙЕудкxжсЩЯЕФЭждВCЙ§Еу![]() ЃЌFЮЊCЕФгвНЙЕуЃЌЁбFЕФЗНГЬЮЊ
ЃЌFЮЊCЕФгвНЙЕуЃЌЁбFЕФЗНГЬЮЊ![]()
ЃЈ1ЃЉЧѓCЕФЗНГЬЃЛ
ЃЈ2ЃЉШєжБЯп![]()
![]() гыЁбOЯрЧаЃЌгыЁбFНЛгкMЁЂNСНЕуЃЌгыCНЛгкPЁЂQСНЕуЃЌЦфжаMЁЂPдкЕквЛЯѓЯоЃЌМЧЁбOЕФУцЛ§ЮЊ
гыЁбOЯрЧаЃЌгыЁбFНЛгкMЁЂNСНЕуЃЌгыCНЛгкPЁЂQСНЕуЃЌЦфжаMЁЂPдкЕквЛЯѓЯоЃЌМЧЁбOЕФУцЛ§ЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ШЁзюДѓжЕЪБЃЌжБЯпlЕФЗНГЬ.
ШЁзюДѓжЕЪБЃЌжБЯпlЕФЗНГЬ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈБОаЁЬтТњЗж13ЗжЃЉ
вбжЊКЏЪ§![]() ЃЌ
ЃЌ![]() ЃЈЦфжа
ЃЈЦфжа![]() ЃЉЃЌЦфВПЗжЭМЯёШчЭМЫљЪО.
ЃЉЃЌЦфВПЗжЭМЯёШчЭМЫљЪО.
ЃЈIЃЉЧѓ![]() ЕФНтЮіЪНЃЛ
ЕФНтЮіЪНЃЛ
ЃЈIIЃЉЧѓКЏЪ§![]() дкЧјМф
дкЧјМф![]() ЩЯЕФзюДѓжЕМАЯргІЕФ
ЩЯЕФзюДѓжЕМАЯргІЕФ![]() жЕЁЃ
жЕЁЃ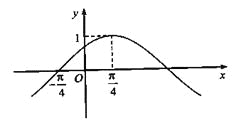
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкШ§Ртжљ![]() жаЃЌ
жаЃЌ![]() ЃЌЖЅЕу
ЃЌЖЅЕу![]() дкЕзУц
дкЕзУц![]() ЩЯЕФЩфгАЧЁЮЊЕу
ЩЯЕФЩфгАЧЁЮЊЕу![]() ЃЌЧв
ЃЌЧв![]()

ЃЈ1ЃЉжЄУїЃКЦНУц![]()
![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧѓРт![]() гы
гы![]() ЫљГЩЕФНЧЕФДѓаЁЃЛ
ЫљГЩЕФНЧЕФДѓаЁЃЛ
ЃЈ3ЃЉШєЕу![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌВЂЧѓГіЖўУцНЧ
ЕФжаЕуЃЌВЂЧѓГіЖўУцНЧ![]() ЕФЦНУцНЧЕФгрЯвжЕЃЎ
ЕФЦНУцНЧЕФгрЯвжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌвбжЊЭждВ
жаЃЌвбжЊЭждВ![]() ЃК
ЃК ![]() ЕФРыаФТЪ
ЕФРыаФТЪ![]() ЃЌзѓЖЅЕуЮЊ
ЃЌзѓЖЅЕуЮЊ![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зїаБТЪЮЊ
зїаБТЪЮЊ![]() ЕФжБЯп
ЕФжБЯп![]() НЛЭждВ
НЛЭждВ![]() гкЕу
гкЕу![]() ЃЌНЛ
ЃЌНЛ![]() жсгкЕу
жсгкЕу![]() ЃЎ
ЃЎ

ЃЈ1ЃЉЧѓЭждВ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉвбжЊ![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌЪЧЗёДцдкЖЈЕу
ЕФжаЕуЃЌЪЧЗёДцдкЖЈЕу![]() ЃЌЖдгкШЮвтЕФ
ЃЌЖдгкШЮвтЕФ![]() ЖМга
ЖМга![]() ЃЌШєДцдкЃЌЧѓГіЕу
ЃЌШєДцдкЃЌЧѓГіЕу![]() ЕФ
ЕФ
зјБъЃЛШєВЛДцдкЫЕУїРэгЩЃЛ
ЃЈ3ЃЉШєЙ§![]() ЕузїжБЯп
ЕузїжБЯп![]() ЕФЦНааЯпНЛЭждВ
ЕФЦНааЯпНЛЭждВ![]() гкЕу
гкЕу![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФзюаЁжЕЃЎ
ЕФзюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com