
【题目】在直角坐标系![]() 中,圆
中,圆![]() 的普通方程为
的普通方程为![]() .在以坐标原点为极点,
.在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出圆![]() 的参数方程和直线
的参数方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 在
在![]() 上,点Q在
上,点Q在![]() 上,求
上,求![]() 的最小值及此时点
的最小值及此时点![]() 的直角坐标.
的直角坐标.
【答案】(1)圆![]() 的参数方程:
的参数方程: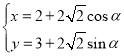 ,直线
,直线![]() :
:![]() ;(2)
;(2)![]() ,此时点
,此时点![]() 的坐标为
的坐标为![]()
【解析】
(1)整理圆![]() 的方程为
的方程为![]() ,即可写出参数方程,利用
,即可写出参数方程,利用![]() 将直线方程写为直角坐标方程即可;
将直线方程写为直角坐标方程即可;
(2)法一:利用参数方程设曲线![]() 上的点
上的点![]() ,利用点到直线距离公式可得
,利用点到直线距离公式可得![]() ,则根据三角函数的性质求处最值,并将
,则根据三角函数的性质求处最值,并将![]() 代回求得坐标;
代回求得坐标;
法二:![]() 为圆心到直线距离减去半径,再利用弦与直线垂直的性质得
为圆心到直线距离减去半径,再利用弦与直线垂直的性质得![]() 所在直线为
所在直线为![]() ,联立直线与圆的方程即可求得交点
,联立直线与圆的方程即可求得交点![]() 的坐标
的坐标
(1)圆![]() 的方程可化为
的方程可化为![]() ,圆心为
,圆心为![]() ,半径为
,半径为![]() ,
,
∴圆![]() 的参数方程为
的参数方程为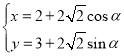 (
(![]() 为参数),
为参数),
直线![]() 的极坐标方程可化为
的极坐标方程可化为![]() ,
,
∵![]() ,∴直线
,∴直线![]() 的直角坐标方程为
的直角坐标方程为![]()
(2)法一:设曲线![]() 上的点
上的点![]() ,
,
点![]() 到直线
到直线![]() :
:![]() 的距离:
的距离:
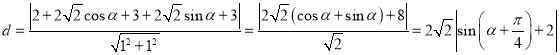 ,
,
当![]() 时,
时,![]() ,
,
此时点![]() 的坐标为
的坐标为![]() ,所以
,所以![]() ,此时点
,此时点![]() 的坐标为
的坐标为![]()
法二:曲线![]() 是以
是以![]() 为圆心,半径为
为圆心,半径为![]() 的圆,
的圆,
圆心![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
所以![]() ,
,
此时直线![]() 经过圆心
经过圆心![]() ,且与直线
,且与直线![]() 垂直,
垂直,
![]() ,所以
,所以![]() ,
,![]() 所在直线方程为
所在直线方程为![]() ,即
,即![]() ,
,
联立直线和圆的方程![]() ,解得
,解得![]() 或
或![]() ,
,
当![]() 取得最小值时,点
取得最小值时,点![]() 的坐标为
的坐标为![]() ,
,
所以![]() ,此时点
,此时点![]() 的坐标为
的坐标为![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】众所周知的“太极图”,其形状如对称的阴阳两鱼互抱在一起,因而也被称为“阴阳鱼太极图”.如图是放在平面直角坐标系中的“太极图”,整个图形是一个圆形,其中黑色阴影区域在y轴右侧部分的边界为一个半圆.给出以下命题:
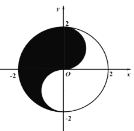
①在太极图中随机取一点,此点取自黑色阴影部分的概率是![]() ;
;
②当![]() 时,直线
时,直线![]() 与黑色阴影部分有公共点;
与黑色阴影部分有公共点;
③黑色阴影部分中一点![]() ,则
,则![]() 的最大值为2.
的最大值为2.
其中所有正确结论的序号是( )
A.①B.②C.①③D.①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 过点
过点![]() ,过坐标原点
,过坐标原点![]() 作两条互相垂直的射线与椭圆
作两条互相垂直的射线与椭圆![]() 分别交于
分别交于![]() ,
,![]() 两点.
两点.
(1)证明:当![]() 取得最小值时,椭圆
取得最小值时,椭圆![]() 的离心率为
的离心率为![]() .
.
(2)若椭圆![]() 的焦距为2,是否存在定圆与直线
的焦距为2,是否存在定圆与直线![]() 总相切?若存在,求定圆的方程;若不存在,请说明理由.
总相切?若存在,求定圆的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
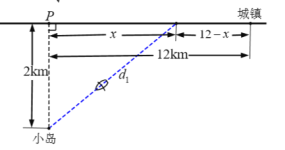
【题目】如图所示,一座小岛距离海岸线上最近的P点的距离是2km,从P点沿海岸正东12km处有一个城镇.假设一个人驾驶的小船的平均速度为![]() ,步行的速度为
,步行的速度为![]() ,时间t(单位:h)表示他从小岛到城镇的时间,x(单位:km)表示此人将船停在海岸处距P点的距离.设
,时间t(单位:h)表示他从小岛到城镇的时间,x(单位:km)表示此人将船停在海岸处距P点的距离.设![]()
![]() ,则( )
,则( )
A.函数![]() 为减函数B.
为减函数B.![]()
C.当![]() 时,此人从小岛到城镇花费的时间最少D.当
时,此人从小岛到城镇花费的时间最少D.当![]() 时,此人从小岛到城镇花费的时间不超过3h
时,此人从小岛到城镇花费的时间不超过3h
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() ,直线
,直线![]() 截抛物线
截抛物线![]() 所得弦长为
所得弦长为![]() .
.
(1)求![]() 的值;
的值;
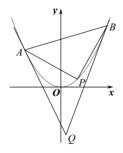
(2)若直角三角形![]() 的三个顶点在抛物线
的三个顶点在抛物线![]() 上,且直角顶点
上,且直角顶点![]() 的横坐标为1,过点
的横坐标为1,过点![]() 、
、![]() 分别作抛物线
分别作抛物线![]() 的切线,两切线相交于点
的切线,两切线相交于点![]() .
.
①若直线![]() 经过点
经过点![]() ,求点
,求点![]() 的纵坐标;
的纵坐标;
②求![]() 的最大值及此时点
的最大值及此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 是定义在
是定义在![]() 上且满足如下条件的函数
上且满足如下条件的函数![]() 组成的集合:①对任意的
组成的集合:①对任意的![]() ,都有
,都有![]() ②存在常数
②存在常数![]() 使得对任意的
使得对任意的![]() ,都有
,都有![]() .
.
(1)设![]() 问
问![]() 是否属于
是否属于![]() ?说明理由;
?说明理由;
(2)若![]() 如果存在
如果存在![]() 使得
使得![]() 证明:这样的
证明:这样的![]() 是唯一的;
是唯一的;
(3)设![]() 且
且![]() 试求
试求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com