练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数，若函数有四个零点，则的取值范围是（ ）

    A.B.C.D.

    【答案】C

    【解析】

    由题意易知，时不满足题意.当且时，为开口向上，对称轴为的二次函数，最多两个零点，当且时，，当时单调递增，当时单调递减，最多两个零点，若使得函数有四个零点，则需，求解即可.

    当时，，函数无零点，舍去.

    当且时，

    为开口向下，对称轴为的二次函数，

    ，.

    则时，函数与轴只有一个交点.

    当且时，.

    函数在上单调递增，.

    则时，函数与轴无交点.

    则当时，函数有一个零点.与题意不符，舍去.

    当且时.

    为开口向上，对称轴为的二次函数.

    ，.

    函数在最多有两个零点

    当且时.

    .

    当时单调递增，当时单调递减，

    函数在最多有两个零点

    若使得函数有四个零点，则需.

    即，解得.

    故选：C

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知数列满足,.

    (1)若为递增数列,且成等差数列,求的值;

    (2)若,且是递增数列,是递减数列,求数列的通项公式.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知是奇函数的导函数，，当时，，则使得成立的的取值范围是（ ）

    A. B.

    C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设A，B两点的坐标分别为（﹣1，0），（1，0）.条件甲：A、B、C三点构成以∠C为钝角的三角形；条件乙：点C的坐标是方程x2+2y2=1（y≠0）的解，则甲是乙的（　　）

    A.充分不必要条件B.必要不充分条件

    C.充要条件D.既不充分又不必要条件

    查看答案和解析>>

    科目：高中数学 来源： 题型：

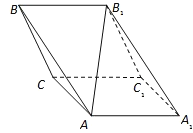
    【题目】斜三棱柱ABC﹣A1B1C1，已知侧面BB1C1C与底面ABC垂直且∠BCA=90°，∠B1BC=60°，BC=BB1=2，若二面角A﹣B1B﹣C为30°

    （1）求AB1与平面BB1C1C所成角的正切值；

    （2）在平面AA1B1B内找一点P，使三棱锥P﹣BB1C为正三棱锥，并求P到平面BB1C距离.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了解某中学学生对《中华人民共和国交通安全法》的了解情况，调查部门在该校进行了一次问卷调查（共12道题），从该校学生中随机抽取40人，统计了每人答对的题数，将统计结果分成，，，，，六组，得到如下频率分布直方图.

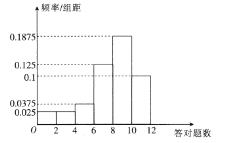
    （1）若答对一题得10分，未答对不得分，估计这40人的成绩的平均分（同一组中的数据用该组区间的中点值作代表）；

    （2）若从答对题数在内的学生中随机抽取2人，求恰有1人答对题数在内的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，圆的普通方程为．在以坐标原点为极点，轴正半轴为极轴的极坐标系中，直线的极坐标方程为．

    （1）写出圆的参数方程和直线的直角坐标方程；

    （2）设点在上，点Q在上，求的最小值及此时点的直角坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题满分13分）

    已知函数，（其中），其部分图像如图所示.

    （I）求的解析式；

    （II）求函数在区间上的最大值及相应的值。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设椭圆C的方程为，O为坐标原点，A为椭团的上顶点，为其右焦点，D是线段的中点，且.

    （1）求椭圆C的方程；

    （2）过坐标原点且斜率为正数的直线交椭圆C于P，Q两点，分别作轴，轴，垂足分别为E，F，连接，并延长交椭圆C于点M，N两点.

    （ⅰ）判断的形状；

    （ⅱ）求四边形面积的最大值.

    查看答案和解析>>

    同步练习册答案