
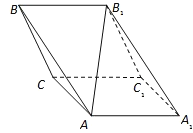
【题目】斜三棱柱ABC﹣A1B1C1,已知侧面BB1C1C与底面ABC垂直且∠BCA=90°,∠B1BC=60°,BC=BB1=2,若二面角A﹣B1B﹣C为30°
(1)求AB1与平面BB1C1C所成角的正切值;
(2)在平面AA1B1B内找一点P,使三棱锥P﹣BB1C为正三棱锥,并求P到平面BB1C距离.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由侧面BB1C1C与底面ABC垂直且∠BCA=90°知AC⊥平面BB1C1C,则有∠AB1C为AB1与平面BB1C1C所成的角,连接B1C,则∠AB1C为AB1与平面BB1C1C所成的角,在Rt△ACB1中可求得tan∠AB1C.
(2)在AD上取点P,使AP=2PD,则P点为所求,在CD上取点O,使CO=2OD,连PO,则易知三棱锥P﹣BB1C为正三棱锥,故可求.
(1)由侧面BB1C1C与底面ABC垂直且∠BCA=90°知AC⊥平面BB1C1C,
取BB1的中点D,AC⊥平面BB1C1C,
∴AC⊥BB1,
∴BB1⊥平面ADC,
∴AD⊥BB1,
∴∠CDA为二面角A﹣BB1﹣C的平面角,∴∠CDA=30°,
∵CD=![]() ,∴AC=1,
,∴AC=1,
连接B1C,则∠AB1C为AB1与平面BB1C1C所成的角,
在Rt△ACB1中tan∠AB1C=![]() ,
,
(2)在AD上取点P,使AP=2PD,则P点为所求,
在CD上取点O,使CO=2OD,连PO,
则PO∥AC,且PO=![]() ,
,
∵AO⊥平面BB1C,
∴PO⊥平面BB1C 且 BB1C为等边三角形,
∴三棱锥P﹣BB1C为正三棱锥,
且P到平面BB1C的距离为PO,PO=![]() .
.


 互动英语系列答案
互动英语系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以O为极点,x轴非负半轴为极轴建立极坐标系圆C的极坐标方程为
中,以O为极点,x轴非负半轴为极轴建立极坐标系圆C的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为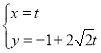 (t为参数),直线
(t为参数),直线![]() 和圆C交于A,B两点,P是圆C上不同于A,B的任意一点.
和圆C交于A,B两点,P是圆C上不同于A,B的任意一点.
(1)求圆C及直线![]() 的直角坐标方程;
的直角坐标方程;
(2)求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合![]() 、
、![]() 均为实数集
均为实数集![]() 的子集,记:
的子集,记:![]() ;
;
(1)已知![]() ,
,![]() ,试用列举法表示
,试用列举法表示![]() ;
;
(2)设![]() ,当
,当![]() ,且
,且![]() 时,曲线
时,曲线![]() 的焦距为
的焦距为![]() ,如果
,如果![]() ,
,![]() ,设
,设![]() 中的所有元素之和为
中的所有元素之和为![]() ,对于满足
,对于满足![]() ,且
,且![]() 的任意正整数
的任意正整数![]() 、
、![]() 、
、![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的最大值;
的最大值;
(3)若整数集合![]() ,则称
,则称![]() 为“自生集”,若任意一个正整数均为整数集合
为“自生集”,若任意一个正整数均为整数集合![]() 的某个非空有限子集中所有元素的和,则称
的某个非空有限子集中所有元素的和,则称![]() 为“
为“![]() 的基底集”,问:是否存在一个整数集合既是自生集又是
的基底集”,问:是否存在一个整数集合既是自生集又是![]() 的基底集?请说明理由.
的基底集?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 过点
过点![]() ,过坐标原点
,过坐标原点![]() 作两条互相垂直的射线与椭圆
作两条互相垂直的射线与椭圆![]() 分别交于
分别交于![]() ,
,![]() 两点.
两点.
(1)证明:当![]() 取得最小值时,椭圆
取得最小值时,椭圆![]() 的离心率为
的离心率为![]() .
.
(2)若椭圆![]() 的焦距为2,是否存在定圆与直线
的焦距为2,是否存在定圆与直线![]() 总相切?若存在,求定圆的方程;若不存在,请说明理由.
总相切?若存在,求定圆的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() ,直线
,直线![]() 截抛物线
截抛物线![]() 所得弦长为
所得弦长为![]() .
.
(1)求![]() 的值;
的值;
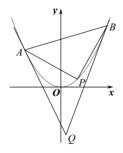
(2)若直角三角形![]() 的三个顶点在抛物线
的三个顶点在抛物线![]() 上,且直角顶点
上,且直角顶点![]() 的横坐标为1,过点
的横坐标为1,过点![]() 、
、![]() 分别作抛物线
分别作抛物线![]() 的切线,两切线相交于点
的切线,两切线相交于点![]() .
.
①若直线![]() 经过点
经过点![]() ,求点
,求点![]() 的纵坐标;
的纵坐标;
②求![]() 的最大值及此时点
的最大值及此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】黄冈“一票通”景区旅游年卡,是由黄冈市旅游局策划,黄冈市大别山旅游公司推出的一项惠民工程.持有旅游年卡一年内可不限次畅游全市19家签约景区.为合理配置旅游资源,现对已游览某签约景区的游客进行满意度调查.随机抽取100位游客进行调查评分(满分100分),评分的频率分布直方图如图.
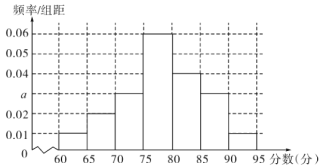
(1)求a的值并估计评分的平均数;
(2)为了了解游客心声,调研机构用分层抽样的方法从评分为![]() ,
,![]() 的游客中抽取了6名,听取他们对该景区建设的建议.现从这6名游客中选取2人,求这2人中至少有一个人的评分在
的游客中抽取了6名,听取他们对该景区建设的建议.现从这6名游客中选取2人,求这2人中至少有一个人的评分在![]() 内的概率;
内的概率;
(3)为更广泛了解游客想法,调研机构对所有评分从低到高排序的前86%游客进行了网上问卷调查并随调查表赠送小礼品,估计收到问卷调查表的游客的最高分数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com