
【题目】黄冈“一票通”景区旅游年卡,是由黄冈市旅游局策划,黄冈市大别山旅游公司推出的一项惠民工程.持有旅游年卡一年内可不限次畅游全市19家签约景区.为合理配置旅游资源,现对已游览某签约景区的游客进行满意度调查.随机抽取100位游客进行调查评分(满分100分),评分的频率分布直方图如图.
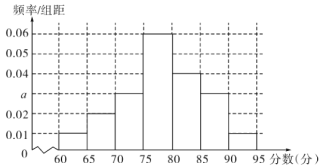
(1)求a的值并估计评分的平均数;
(2)为了了解游客心声,调研机构用分层抽样的方法从评分为![]() ,
,![]() 的游客中抽取了6名,听取他们对该景区建设的建议.现从这6名游客中选取2人,求这2人中至少有一个人的评分在
的游客中抽取了6名,听取他们对该景区建设的建议.现从这6名游客中选取2人,求这2人中至少有一个人的评分在![]() 内的概率;
内的概率;
(3)为更广泛了解游客想法,调研机构对所有评分从低到高排序的前86%游客进行了网上问卷调查并随调查表赠送小礼品,估计收到问卷调查表的游客的最高分数.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据频率和为1即可求得a的值;根据平均数的求法,代入即可求得评分的平均数.
(2)在![]() ,
,![]() 的游客中抽取了6名,其中在
的游客中抽取了6名,其中在![]() 抽取2人,在
抽取2人,在![]() 中抽取4人,根据古典概型概率求法,列举出所有可能,即可求得至少有一个人的评分在
中抽取4人,根据古典概型概率求法,列举出所有可能,即可求得至少有一个人的评分在![]() 内的概率.
内的概率.
(3)先求得从低分到高分排列, 最低的前86%最高分落在的评分区间,利用百分比即可求得最高分.
(1)由![]() ,得
,得![]() .
.
游客评分的平均数为:
![]() (2)抽取的6名游客,评分在
(2)抽取的6名游客,评分在![]() 内的4个,记为1,2,3,4,
内的4个,记为1,2,3,4,
在![]() 内的2个,记为5,6
内的2个,记为5,6
从这6人随机选取2人,有12,13,14,15,16,23,24,25,26,34,35,36,45,35,56共15中选法,其中至少有一个在![]() 内有15,16,25,26,35,36,45,46,56共9种
内有15,16,25,26,35,36,45,46,56共9种
由古典概型,![]() .
.
(3)评分低于85分的概率为![]()
故评分最低的前86%最高分在![]()
设最高分为x,由![]()
得![]()


科目:高中数学 来源: 题型:
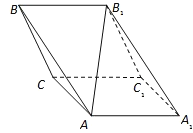
【题目】斜三棱柱ABC﹣A1B1C1,已知侧面BB1C1C与底面ABC垂直且∠BCA=90°,∠B1BC=60°,BC=BB1=2,若二面角A﹣B1B﹣C为30°
(1)求AB1与平面BB1C1C所成角的正切值;
(2)在平面AA1B1B内找一点P,使三棱锥P﹣BB1C为正三棱锥,并求P到平面BB1C距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已过抛物线![]() :
:![]() 的焦点
的焦点![]() 作直线
作直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
,![]() 两点,以
两点,以![]() ,
,![]() 两点为切点作抛物线的切线,两条直线交于
两点为切点作抛物线的切线,两条直线交于![]() 点.
点.
(1)当直线![]() 平行于
平行于![]() 轴时,求点
轴时,求点![]() 的坐标;
的坐标;
(2)当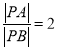 时,求直线
时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为椭圆
的焦点为椭圆![]() 的右焦点,且椭圆长轴的长为4,
的右焦点,且椭圆长轴的长为4,![]() 、
、![]() 是椭圆上的两点;
是椭圆上的两点;
(1)求椭圆标准方程;
(2)若直线![]() 经过点
经过点![]() ,且
,且![]() ,求直线
,求直线![]() 的方程;
的方程;
(3)若动点![]() 满足:
满足:![]() ,直线
,直线![]() 与
与![]() 的斜率之积为
的斜率之积为![]() ,是否存在两个定点
,是否存在两个定点![]() 、
、![]() ,使得
,使得![]() 为定值?若存在,求出
为定值?若存在,求出![]() 、
、![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆C的方程为![]() ,O为坐标原点,A为椭团的上顶点,
,O为坐标原点,A为椭团的上顶点,![]() 为其右焦点,D是线段
为其右焦点,D是线段![]() 的中点,且
的中点,且![]() .
.
(1)求椭圆C的方程;
(2)过坐标原点且斜率为正数的直线交椭圆C于P,Q两点,分别作![]() 轴,
轴,![]() 轴,垂足分别为E,F,连接
轴,垂足分别为E,F,连接![]() ,
,![]() 并延长交椭圆C于点M,N两点.
并延长交椭圆C于点M,N两点.
(ⅰ)判断![]() 的形状;
的形状;
(ⅱ)求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 是公差
是公差![]() 的等差数列,且
的等差数列,且![]() .
.
(1)求![]() 的前
的前![]() 项的和
项的和![]() ;
;
(2)若![]() ,问在数列
,问在数列![]() 中是否存在一项
中是否存在一项![]() (
(![]() 是正整数),使得
是正整数),使得![]() 成等比数列,若存在,求出
成等比数列,若存在,求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(3)若存在自然数![]() (
(![]() 是正整数),满足
是正整数),满足![]() ,使得
,使得![]() 成等比数列,求所有整数
成等比数列,求所有整数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]() ,且
,且![]() 中的元素个数
中的元素个数![]() 大于等于5.若集合
大于等于5.若集合![]() 中存在四个不同的元素
中存在四个不同的元素![]() ,使得
,使得![]() ,则称集合
,则称集合![]() 是“关联的”,并称集合
是“关联的”,并称集合![]() 是集合
是集合![]() 的“关联子集”;若集合
的“关联子集”;若集合![]() 不存在“关联子集”,则称集合
不存在“关联子集”,则称集合![]() 是“独立的”.
是“独立的”.
![]() 分别判断集合
分别判断集合![]() 和集合
和集合![]() 是“关联的”还是“独立的”?若是“关联的”,写出其所有的关联子集;
是“关联的”还是“独立的”?若是“关联的”,写出其所有的关联子集;
![]() 已知集合
已知集合![]() 是“关联的”,且任取集合
是“关联的”,且任取集合![]() ,总存在
,总存在![]() 的关联子集
的关联子集![]() ,使得
,使得![]() .若
.若![]() ,求证:
,求证:![]() 是等差数列;
是等差数列;
![]() 集合
集合![]() 是“独立的”,求证:存在
是“独立的”,求证:存在![]() ,使得
,使得![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com