【题目】已过抛物线
：
的焦点
作直线
交抛物线于
，
两点，以，两点为切点作抛物线的切线，两条直线交于
点.
（1）当直线平行于
轴时，求点的坐标；
（2）当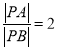
时，求直线的方程.
【答案】（1）
，（2）
【解析】
（1）依题
的方程为
，联立抛物线方程可得
，
，利用导数求出
在
，
处的切线，再联立切线方程即可求出
点坐标.
（2）设的方程为
，
，
，利用切线方程联系即可求出
.
法一：根据弦长公式可得，
， 
，再根据
，将
代入即可求出结果.
法二：依题：
，化简可得
，结合，进而求出结果.得
（1）依题可知
，当直线平行于
轴时，则的方程为，
所以可得，，又
；
所以在，处的切线分别为：
，
，即
，
，
联立两切线可得
，所以.
（2）设的方程为，，，
则联立有
，所以
，
在处的切线为：
，
同理可得，在处切线：
，
联立有：
，即点.
法一：
，
同理可得：
，
所以
，又因为，
所以解得
，所以
，得
，
或
，
.
所以直线方程为：.
法二：
依题：
，
解得，结合得，或，.
所以直线方程为：.
科学实验活动册系列答案科目：高中数学 来源： 题型：
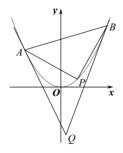
【题目】已知抛物线
：
，直线
截抛物线所得弦长为
.
（1）求
的值；
（2）若直角三角形
的三个顶点在抛物线上，且直角顶点
的横坐标为1，过点
、
分别作抛物线的切线，两切线相交于点
.
①若直线
经过点
，求点的纵坐标；
②求
的最大值及此时点的坐标.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】
是定义在
上且满足如下条件的函数
组成的集合：①对任意的
，都有
②存在常数
使得对任意的
，都有
.
（1）设
问是否属于？说明理由;
（2）若
如果存在
使得
证明：这样的
是唯一的；
（3）设
且试求
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知等比数列
的公比
，且
，
是
、
的等差中项.
（1）求数列的通项公式；
（2）试比较
与
的大小，并说明理由；
（3）若数列
满足
，在每两个
与
之间都插入
个2，使得数列变成了一个新的数列
，试问：是否存在正整数
，使得数列的前项和
？如果存在，求出的值；如果不存在，说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设函数
的定义域为
，若存在非零实数
满足对任意
，均有
，且
，则称为
上的高调函数. 如果定义域为的函数是奇函数，当
时，
，且为
上的8高调函数，那么实数
的取值范围为____.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】黄冈“一票通”景区旅游年卡，是由黄冈市旅游局策划，黄冈市大别山旅游公司推出的一项惠民工程.持有旅游年卡一年内可不限次畅游全市19家签约景区.为合理配置旅游资源，现对已游览某签约景区的游客进行满意度调查.随机抽取100位游客进行调查评分（满分100分），评分的频率分布直方图如图.
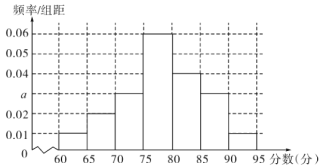
（1）求a的值并估计评分的平均数；
（2）为了了解游客心声，调研机构用分层抽样的方法从评分为
，
的游客中抽取了6名，听取他们对该景区建设的建议.现从这6名游客中选取2人，求这2人中至少有一个人的评分在内的概率；
（3）为更广泛了解游客想法，调研机构对所有评分从低到高排序的前86%游客进行了网上问卷调查并随调查表赠送小礼品，估计收到问卷调查表的游客的最高分数.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
在区间
上的最大值为4，最小值为1，记为
.
（1）求实数
，
的值；
（2）若不等式
成立，求实数
的取值范围；
（3）对于任意满足
的自变量
，
，
，…，
，如果存在一个常数
，使得定义在区间
上的一个函数
，
恒成立，则称函数为区间上的有界变差函数，试判断函数
是否是区间
上的有界变差函数，若是，求出
的最小值；若不是，请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
