
分析 (Ⅰ)由由a>0,有f(x)=|x+$\frac{6}{a}$|+|x-a|≥丨(x+$\frac{6}{a}$)-(x-a)丨=$\frac{6}{a}$+a≥2$\sqrt{6}$,即可证明:f(x)≥2$\sqrt{6}$;
(Ⅱ)f(3)<7,当a>3时,f(3)=a+$\frac{6}{a}$,由f(3)<7,求得3<a<6,0<a≤3时,f(3)=6-a+$\frac{6}{a}$,求得2<a≤3,即可求得a的取值范围.
解答 解:(Ⅰ)证明:由a>0,有f(x)=|x+$\frac{6}{a}$|+|x-a|≥丨(x+$\frac{6}{a}$)-(x-a)丨=$\frac{6}{a}$+a≥2$\sqrt{6}$,
当且仅当$\frac{6}{a}$=a,即a=$\sqrt{6}$时,取等号,
∴f(x)≥2$\sqrt{6}$;…(5分)
(Ⅱ)f(3)=3+$\frac{6}{a}$+|3-a|.
当a>3时,f(3)=a+$\frac{6}{a}$,由f(3)<7,得1<a<6,
∴3<a<6.…(8分)
当0<a≤3时,f(3)=6-a+$\frac{6}{a}$,由f(3)<7,得a>2或a<-3,
∴2<a≤3,…(11分)
综上,a的取值范围是(2,6).…(12分)
点评 本题考查含绝对值不等式的解法,考查基本不等式的应用,一元二次不等式不等式的解法,考查分类讨论思想,属于中档题.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:解答题
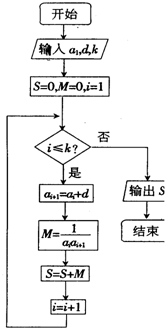 已知数列{an}的各项均为正数,观察程序框图,若k=1,k=5时,分别有S=$\frac{1}{3}$和S=$\frac{5}{11}$.
已知数列{an}的各项均为正数,观察程序框图,若k=1,k=5时,分别有S=$\frac{1}{3}$和S=$\frac{5}{11}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,4) | B. | (0,3) | C. | (0.4) | D. | (3,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com