
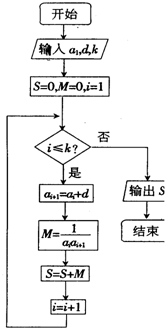
 已知数列{an}的各项均为正数,观察程序框图,若k=1,k=5时,分别有S=$\frac{1}{3}$和S=$\frac{5}{11}$.
已知数列{an}的各项均为正数,观察程序框图,若k=1,k=5时,分别有S=$\frac{1}{3}$和S=$\frac{5}{11}$.分析 (1)根据程序框图得出{an}为等差数列,利用k=1和k=5得出方程组解出a1和d,即可得出an;
(2)使用错位相减法求出Tn.
解答 解:(1)由程序框图可知:{an}为等差数列,
$\frac{1}{{a}_{1}{a}_{2}}$=$\frac{1}{3}$,
$\frac{1}{{a}_{1}{a}_{2}}$+$\frac{1}{{a}_{2}{a}_{3}}$+$\frac{1}{{a}_{3}{a}_{4}}$+$\frac{1}{{a}_{4}{a}_{5}}$+$\frac{1}{{a}_{5}{a}_{6}}$=$\frac{5}{11}$,
∴$\left\{\begin{array}{l}{\frac{1}{d}(\frac{1}{{a}_{1}}-\frac{1}{{a}_{1}+d})=\frac{1}{3}}\\{\frac{1}{d}(\frac{1}{{a}_{1}}-\frac{1}{{a}_{1}+5d})=\frac{5}{11}}\end{array}\right.$,解得:$\left\{\begin{array}{l}{{a}_{1}=1}\\{d=2}\end{array}\right.$或$\left\{\begin{array}{l}{{a}_{1}=-1}\\{d=-2}\end{array}\right.$(舍去),
∴an=1+2(n-1)=2n-1.
(2)bn=(2n-1)•3n,
∴Tn=1×3+3×32+5×33+…+(2n-1)×3n,
∴3Tn=1×32+3×33+5×34+…+(2n-1)×3n+1,
∴$2{T_n}=-3-2({3^2}+{3^3}+…+{3^n})+{3^{n+1}}(2n-1)=6+{3^{n+1}}(2n-2)$,
∴Tn=3+(n-1)•3n+1.
点评 本题考查了程序框图,等差数列的通项公式,错位相减法数列求和.


科目:高中数学 来源: 题型:解答题
| 父母吸烟 | 父母不吸烟 | 总计 | |
| 子女吸烟 | 237 | 83 | |
| 子女不吸烟 | 678 | ||
| 总计 | 1520 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=ln(x2+1) | B. | y=-x2cosx | C. | y=-lg|x| | D. | y=($\frac{1}{2}$)x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 命中环数 | 10环 | 9环 | 8环 | 7环 |
| 概率 | 0.30 | 0.28 | 0.18 | 0.12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com