
| 命中环数 | 10环 | 9环 | 8环 | 7环 |
| 概率 | 0.30 | 0.28 | 0.18 | 0.12 |
分析 设“射中10环”“射中9环”“射中8环”“射中7环”的事件分别为A、B、C、D
(1)在一次射击中射中10环或9环,即射中10环和射中9环,由互斥事件的概率公式,再分别相加即可.
(2)在一次射击中至少射中8环,即射中10环,射中9环,射中8环,再将对应的概率相加即可.
(3)在一次射击中射中环数不足8环,即射中7环和射中7环以下,再利用互斥事件概率计算即可.
解答 解:设“射中10环”“射中9环”“射中8环”“射中7环”的事件分别为A、B、C、D
(1)P(A+B)=P(A)+P(B)=0.30+0.28=0.58,
即射中10环或9环的概率为0.58.
(2)P(A+B+C)=P(A)+P(B)+P(C)=0.30+0.28+0.18=0.76,
即至少射中8环的概率为0.76.
(3)1-P(A+B+C)=1-0.76=0.24,
即射中环数不足8环的概率为0.24.
点评 本题考查了互斥事件有一个发生的概率公式的应用,若A,B互斥,则P(A+B)=P(A)+P(B),当一个事件的正面情况比较多或正面情况难确定时,可考虑对立事件.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
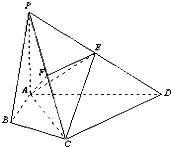 在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2.
在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
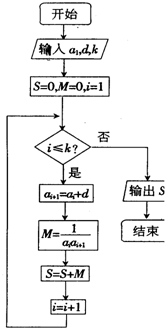 已知数列{an}的各项均为正数,观察程序框图,若k=1,k=5时,分别有S=$\frac{1}{3}$和S=$\frac{5}{11}$.
已知数列{an}的各项均为正数,观察程序框图,若k=1,k=5时,分别有S=$\frac{1}{3}$和S=$\frac{5}{11}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com