
分析 (1)由(x+2)10的展开式的通项公式Tr+1=${C}_{10}^{r}$•2r•xr-1,列方程组,$\left\{\begin{array}{l}{{C}_{10}^{r}{2}^{r}≥{C}_{10}^{r-1}{2}^{r-1}}\\{{C}_{10}^{r}{2}^{r}≥{C}_{10}^{r+1}{2}^{r+1}}\end{array}\right.$,即可求得r的值,即可求得展开式中系数最大的项;
(2)n为奇数,an=${C}_{n}^{\frac{n+1}{2}}$=${C}_{n}^{\frac{n-1}{2}}$,an+1=${C}_{n+1}^{\frac{n+1}{2}}$,an+1=${C}_{n+1}^{\frac{n+1}{2}}$=${C}_{n}^{\frac{n+1}{2}}$+${C}_{n}^{\frac{n-1}{2}}$>an,同理可知:n为偶数,an+1=${C}_{n+1}^{\frac{n}{2}}$=${C}_{n}^{\frac{n}{2}-1}$+${C}_{n}^{\frac{n}{2}}$>an,即可证明:数列{an}单调递增;
(3)${C}_{n}^{k+1}$-${C}_{n}^{k}$=$\frac{n!}{(k+1)!(n-k-1)!}$-$\frac{n!}{k!(n-k)!}$=$\frac{n!}{(k+1)!(n-k)!}$(n-1-2k),当k<$\frac{n-1}{2}$时,${C}_{n}^{k}$<${C}_{n}^{k+1}$,当k>$\frac{n-1}{2}$时,${C}_{n}^{k}$>${C}_{n}^{k+1}$,分别讨论当n为奇数及n为偶数时,根据二项式的展开可知,离首末两端等距离的项相等,且距离越远值越大.
解答 解:(1)由(x+2)10的展开式的通项公式Tr+1=${C}_{10}^{r}$•2r•xr-1,
∴$\left\{\begin{array}{l}{{C}_{10}^{r}{2}^{r}≥{C}_{10}^{r-1}{2}^{r-1}}\\{{C}_{10}^{r}{2}^{r}≥{C}_{10}^{r+1}{2}^{r+1}}\end{array}\right.$,解得:$\frac{19}{3}$≤r≤$\frac{22}{4}$,即r=7,
二项式(x+2)10展开式中系数最大的项T8=${C}_{10}^{7}$x3•27=15360x3;
(2)证明:若n为奇数,则n+1为偶数,an=${C}_{n}^{\frac{n+1}{2}}$=${C}_{n}^{\frac{n-1}{2}}$,an+1=${C}_{n+1}^{\frac{n+1}{2}}$,
∴an+1=${C}_{n+1}^{\frac{n+1}{2}}$=${C}_{n}^{\frac{n+1}{2}}$+${C}_{n}^{\frac{n-1}{2}}$>an,
若n为偶数,则n+1为奇数,an=${C}_{n}^{\frac{n}{2}}$,an+1=${C}_{n+1}^{\frac{n}{2}}$=${C}_{n+1}^{\frac{n}{2}+1}$,
∴an+1=${C}_{n+1}^{\frac{n}{2}}$=${C}_{n}^{\frac{n}{2}-1}$+${C}_{n}^{\frac{n}{2}}$>an,
综上可知:数列{an}单调递增;
(3)数列{C${\;}_{n}^{k}$}(k=0,1,2,…,n)离首末两端等距离的项相等,且距离越远值越大,
证明:${C}_{n}^{k+1}$-${C}_{n}^{k}$=$\frac{n!}{(k+1)!(n-k-1)!}$-$\frac{n!}{k!(n-k)!}$=$\frac{n!}{(k+1)!(n-k)!}$(n-1-2k),
当k<$\frac{n-1}{2}$时,${C}_{n}^{k}$<${C}_{n}^{k+1}$,
当k>$\frac{n-1}{2}$时,${C}_{n}^{k}$>${C}_{n}^{k+1}$,其中k=0,1,2,…,n-1.
若n为奇数,${C}_{n}^{0}$<${C}_{n}^{1}$<${C}_{n}^{2}$<…<${C}_{n}^{\frac{n-3}{2}}$<${C}_{n}^{\frac{n-1}{2}}$,
${C}_{n}^{\frac{n+1}{2}}$>${C}_{n}^{\frac{n+3}{2}}$>…>${C}_{n}^{n-1}$>${C}_{n}^{n}$,
若n为偶数,${C}_{n}^{0}$<${C}_{n}^{1}$<${C}_{n}^{2}$<…<${C}_{n}^{\frac{n-2}{2}}$<${C}_{n}^{\frac{n}{2}}$,
${C}_{n}^{\frac{n}{2}}$>${C}_{n}^{\frac{n+2}{2}}$>…>${C}_{n}^{n-1}$>${C}_{n}^{n}$.
点评 本题考查二项式定理的应用,考查二项式展开式的通项公式及性质,考查分类讨论思想,属于中档题.


科目:高中数学 来源: 题型:选择题
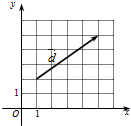 已知向量$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=(0,1),$\overrightarrow{c}$=$\overrightarrow{a}$+λ$\overrightarrow{b}$(λ∈R),向量$\overrightarrow{d}$如图所示,若$\overrightarrow{c}$∥$\overrightarrow{d}$,则λ=( )
已知向量$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=(0,1),$\overrightarrow{c}$=$\overrightarrow{a}$+λ$\overrightarrow{b}$(λ∈R),向量$\overrightarrow{d}$如图所示,若$\overrightarrow{c}$∥$\overrightarrow{d}$,则λ=( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $-\frac{4}{3}$ | D. | $-\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=ln(x2+1) | B. | y=-x2cosx | C. | y=-lg|x| | D. | y=($\frac{1}{2}$)x |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 命中环数 | 10环 | 9环 | 8环 | 7环 |
| 概率 | 0.30 | 0.28 | 0.18 | 0.12 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com