
分析 (1)求出圆心到直线2x-y+m=0的距离,利用直线与圆无公共点,可得d>r,即可得出结论;
(2)由平面几何垂径定理知r2-d2=12,即可得出结论;
(3)由于交点处两条半径互相垂直,弦与过弦两端的半径组成等腰直角三角形,即可得出结论.
解答 解:(1)由已知,圆心为O(0,0),半径r=$\sqrt{5}$,圆心到直线2x-y+m=0的距离d=$\frac{|m|}{\sqrt{4+1}}$=$\frac{|m|}{\sqrt{5}}$,
∵直线与圆无公共点,∴d>r,即$\frac{|m|}{\sqrt{5}}$>$\sqrt{5}$,
∴m>5或m<-5.
故当m>5或m<-5时,直线与圆无公共点.
(2)由平面几何垂径定理知r2-d2=12,即5-$\frac{{m}^{2}}{5}$=1.
得m=±2$\sqrt{5}$,
∴当m=±2$\sqrt{5}$时,直线被圆截得的弦长为2.
(3)由于交点处两条半径互相垂直,
∴弦与过弦两端的半径组成等腰直角三角形,
∴d=$\frac{\sqrt{2}}{2}$r,即$\frac{|m|}{\sqrt{5}}$=$\frac{\sqrt{2}}{2}$•$\sqrt{5}$,
解得m=±$\frac{5\sqrt{2}}{2}$.
故当m=±$\frac{5\sqrt{2}}{2}$时,直线与圆在两交点处的两条半径互相垂直.
点评 本题考查直线与圆的位置关系,考查学生的计算能力,属于中档题.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:高中数学 来源: 题型:解答题
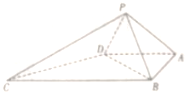 如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD都是等边三角形.
如图,四棱锥P-ABCD中,∠ABC=∠BAD=90°,BC=2AD,△PAB与△PAD都是等边三角形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com