
| A. | 61 | B. | 62 | C. | 63 | D. | 64 |
分析 求出数列的等比与首项,化简a1a2…an,然后求解最值.
解答 解:等比数列{an}满足a1+a3=10,a2+a4=5,
可得q(a1+a3)=5,解得q=$\frac{1}{2}$.
a1+q2a1=10,解得a1=8.
则a1a2…an=a1n•q1+2+3+…+(n-1)=8n•($\frac{1}{2}$)${\;}^{\frac{n(n+1)}{2}}$=2${\;}^{3n-\frac{{n}^{2}-n}{2}}$=${2}^{\frac{7n{-n}^{2}}{2}}$,
当n=3或4时,表达式取得最大值:2${\;}^{\frac{12}{2}}$=26=64.
故选:D.
点评 本题考查数列的性质数列与函数相结合的应用,转化思想的应用,考查计算能力.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
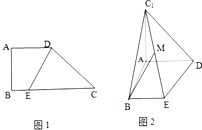 如图1,直角梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=$\frac{1}{2}$BC=1,E是底边BC上的一点,且EC=3BE.现将△CDE沿DE折起到△C1DE的位置,得到如图2所示的四棱锥C1-ABED,且C1A=AB.
如图1,直角梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=$\frac{1}{2}$BC=1,E是底边BC上的一点,且EC=3BE.现将△CDE沿DE折起到△C1DE的位置,得到如图2所示的四棱锥C1-ABED,且C1A=AB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com