练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．为了研究子女与父母吸烟的关系，调查了一千多名青少年及其家长，数据如下：
    父母吸烟父母不吸烟总计
    子女吸烟23783
    子女不吸烟678
    总计1520
    完善上表，并分别利用等高条形图和独立性检验方法判断父母吸烟对子女吸烟是否有影响？

    分析 补充列联表，可得等高条形图，计算KK2，即可得出结论

    解答 解：

    父母吸烟父母不吸烟总计
    子女吸烟23783320
    子女不吸烟6785221200
    总计9156051520

    由图形观察：底面副对角线上两个柱体高度的乘积要大一些，因此可以在某种程度上认为“子女吸烟与父母吸烟有关”．?
    由列联表中的数据得到?
    K2=$\frac{1520×（237×522-83×678）^{2}}{915×605×320×1200}$≈32.52＞6.635．?
    所以在犯错的概率不超过0.001的前提下，认为两者有关系．

    点评 独立性检验的应用的步骤为：根据已知条件将数据归结到一个表格内，列出列联表，再根据列联表中的数据，代入公式计算出k值，然后代入离散系数表，比较即可得到答案．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    4．设$\overrightarrow{a}$，$\overrightarrow{b}$是两个非零向量，则下列命题为真命题的是
    ①若$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为60°，则|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|；
    ②若|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|，则$\overrightarrow{a}$与$\overrightarrow{a}$+$\overrightarrow{b}$的夹角60°；
    ③若|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|-|$\overrightarrow{b}$|，则存在非零实数λ，使得$\overrightarrow{b}$=λ$\overrightarrow{a}$；
    ④若存在非零实数λ，使得$\overrightarrow{b}$=λ$\overrightarrow{a}$，则|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$|-|$\overrightarrow{b}$；
    ⑤若$\overrightarrow{a}$与$\overrightarrow{b}$共线且同向，则|$\overrightarrow{a}$•$\overrightarrow{b}$|=|$\overrightarrow{a}$||$\overrightarrow{b}$|．
    其中的正确的结论是③⑤（写出所有正确结论的序号）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．已知函数f（x）=lnx+$\frac{1}{2}a$x2-（a+1）x（a∈R）．
    （I）a=1时，求函数y=f（x）的零点个数；
    （Ⅱ）当a＞0时，若函数y=f（x）在区间[1．e]上的最小值为-2，求a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．已知函数$f（x）=\left\{\begin{array}{l}{2^x}，x＜1\\ f（x-1），x≥1\end{array}\right.$，则f（log25）=$\frac{5}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．已知z∈C，且|z+3-4i|=1，则|z|的最大值为6，最小值为4．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．已知函数$f（x）=cos（\frac{π}{2}+x）+{sin^2}（\frac{π}{2}+x）$，x∈R，则f（x）的最大值为$\frac{5}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．在△ABC中，角A，B，C所对的边分别为a，b，c，已知a=1，且（1-b）（sinA+sinB）=（c-b）sinC，则△ABC周长的最大值为3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．已知圆锥的底面半径为1，母线长与底面的直径相等，则该圆锥的体积为$\frac{{\sqrt{3}π}}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

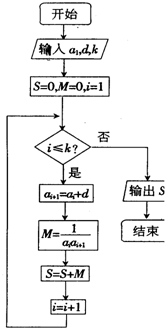    4．已知数列{an}的各项均为正数，观察程序框图，若k=1，k=5时，分别有S=$\frac{1}{3}$和S=$\frac{5}{11}$．
    （1）试求数列{an}的通项公式；
    （2）令bn=3n•an，求数列{bn}的前n项和Tn．

    查看答案和解析>>

    同步练习册答案