
分析 将函数:$f(x)=cos(\frac{π}{2}+x)+{sin^2}(\frac{π}{2}+x)$进行化简得f(x)=-sinx+cos2x,转化成二次函数求其最大值.
解答 解:由函数$f(x)=cos(\frac{π}{2}+x)+{sin^2}(\frac{π}{2}+x)$,
化简:f(x)=-sinx+cos2x
=1-sin2x-sinx
=-(sinx+$\frac{1}{2}$)$+\frac{5}{4}$
当sinx=$\frac{1}{2}$时,f(x)的最大值为$\frac{5}{4}$
故答案为$\frac{5}{4}$.
点评 本题主要考查了三角函数公式的化简能力.从而转化成二次函数求其最大值是解决本题的关键.属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 43米 | B. | 78米 | C. | 118米 | D. | 121米 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{3}-{y^2}=1$ | B. | ${y^2}-\frac{x^2}{3}=1$ | C. | $\frac{x^2}{12}-\frac{y^2}{4}=1$ | D. | $\frac{y^2}{12}-\frac{x^2}{4}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 父母吸烟 | 父母不吸烟 | 总计 | |
| 子女吸烟 | 237 | 83 | |
| 子女不吸烟 | 678 | ||
| 总计 | 1520 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 6 | C. | 9 | D. | 15 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
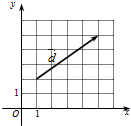 已知向量$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=(0,1),$\overrightarrow{c}$=$\overrightarrow{a}$+λ$\overrightarrow{b}$(λ∈R),向量$\overrightarrow{d}$如图所示,若$\overrightarrow{c}$∥$\overrightarrow{d}$,则λ=( )
已知向量$\overrightarrow{a}$=(1,0),$\overrightarrow{b}$=(0,1),$\overrightarrow{c}$=$\overrightarrow{a}$+λ$\overrightarrow{b}$(λ∈R),向量$\overrightarrow{d}$如图所示,若$\overrightarrow{c}$∥$\overrightarrow{d}$,则λ=( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $-\frac{4}{3}$ | D. | $-\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=ln(x2+1) | B. | y=-x2cosx | C. | y=-lg|x| | D. | y=($\frac{1}{2}$)x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com