
分析 讨论对称轴与区间的关系判断函数的对称性,列出方程解出a.
解答 解:二次函数f(x)=x2+2ax+1的对称轴为x=-a,开口向上.
(1)若-a≤-1,即a≥1,则f(x)在[-1,2]上是增函数,
∴f(-1)=2-2a=4,解得a=-2(舍).
(2)若-a≥2,即a≤-2时,f(x)在[-1,2]上是减函数,
∴f(2)=5+4a=-4,解得a=-$\frac{9}{4}$.
(3),若-1<-a<2,即-2<a<1,则f(x)在[-1,2]上先减后增,
∴f(-a)=-a2+1=-4,解得a=-$\sqrt{5}$(舍)或a=$\sqrt{5}$(舍).
综上,a=-$\frac{9}{4}$.
点评 本题考查了二次函数的单调性,属于中档题.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
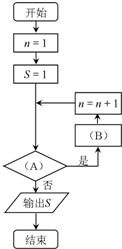 已知数列{an},a1=1,an+1=an+n,计算数列{an}的第20项.现已给出该问题算法的程序框图(如图所示).为使之能完成上述的算法功能,则在如图判断框中(A)处和(B)处依次应填上合适的语句是( )
已知数列{an},a1=1,an+1=an+n,计算数列{an}的第20项.现已给出该问题算法的程序框图(如图所示).为使之能完成上述的算法功能,则在如图判断框中(A)处和(B)处依次应填上合适的语句是( )| A. | n≤20,S=S-n | B. | n≤20,S=S+n | C. | n≤19,S=S-n | D. | n≤19,S=S+n |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
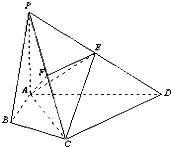 在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2.
在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
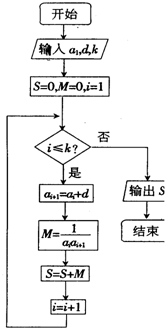 已知数列{an}的各项均为正数,观察程序框图,若k=1,k=5时,分别有S=$\frac{1}{3}$和S=$\frac{5}{11}$.
已知数列{an}的各项均为正数,观察程序框图,若k=1,k=5时,分别有S=$\frac{1}{3}$和S=$\frac{5}{11}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com