
分析 根据三角函数符号和象限之间的关系进行判断即可.
利用“1=sin2θ+cos2θ”,再将弦化切,利用条件,即可求得结论.
解答 解:∵|cos$\frac{α}{2}$|=-cos$\frac{α}{2}$,
∴cos$\frac{α}{2}$≤0,
∵α角属于第二象限,
∴$\frac{α}{2}$属于第一或三象限,
∴$\frac{α}{2}$角属于第三象限,
∵tanθ=2,∴$\frac{si{n}^{2}θ+sinθcosθ-2co{s}^{2}θ}{si{n}^{2}θ+co{s}^{2}θ}$=$\frac{ta{n}^{2}θ+tanθ-2}{ta{n}^{2}θ+1}$=$\frac{{2}^{2}+2-2}{{2}^{2}+1}$=$\frac{4}{5}$,
故答案为:三,$\frac{4}{5}$.
点评 本题重点考查考查三角函数角的象限的确定,同角三角函数间基本关系,解题的关键是利用“1=sin2θ+cos2θ”,再将弦化切,属于基础题.


科目:高中数学 来源: 题型:填空题
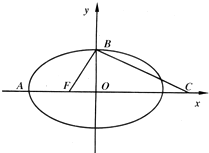 如图,F是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的一个焦点,A,B是椭圆的两个顶点,椭圆的离心率为$\frac{1}{2}$.点C在x轴上,BC⊥BF,B,C,F三点确定的圆M恰好与直线l1:$x+\sqrt{3}y+3=0$相切.则椭圆的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$.
如图,F是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的一个焦点,A,B是椭圆的两个顶点,椭圆的离心率为$\frac{1}{2}$.点C在x轴上,BC⊥BF,B,C,F三点确定的圆M恰好与直线l1:$x+\sqrt{3}y+3=0$相切.则椭圆的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
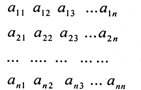 如图表:现有n2(n≥4)个正数排列成n行n列方阵,符号aij(1≤i≤n,1≤j≤n,i,j∈N*)表示位于第i行第j列的正数.已知每一行的数成等差数列,每一列的数成等比数列,且各列数的公比都相等.若a11=2,a24=a32=16,则aij=2i•j.
如图表:现有n2(n≥4)个正数排列成n行n列方阵,符号aij(1≤i≤n,1≤j≤n,i,j∈N*)表示位于第i行第j列的正数.已知每一行的数成等差数列,每一列的数成等比数列,且各列数的公比都相等.若a11=2,a24=a32=16,则aij=2i•j.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com