f(x)和g(x)都是定义在集合M上的函数,对于任意的x∈M,都有f(g(x))=g(f(x))成立,称函数f(x)与g(x)在M上互为“H函数”.
(1)若函数f(x)=ax+b,g(x)=mx+n,f(x)与g(x)互为“H函数”,证明:f(n)=g(b)
(2)若集合M=[-2,2],函数f(x)=x2,g(x)=cosx,判断函数f(x)与g(x)在M上是否互为“H函数”,并说明理由.
(3)函数f(x)=ax(a>0且a≠1),g(x)=x+1在集合M上互为“H函数”,求a的取值范围及集合M.
(1)证明:∵f(x)=ax+b,
g(x)=mx+n,f(x)与g(x)互为“H函数”,
∴对于?x∈R,f(g(x))=g(f(x))成立.
即ag(x)+b=mf(x)+n恒成立…
∴max+an+b=amx+mb+n,…
∴an+b=mb+n,
∴f(n)=g(b).…
(2)解:假设函数f(x)与g(x)互为“H函数”,
则对于任意的x∈Mf(g(x))=g(f(x))恒成立.
即cosx
2=cos
2x,对于任意x∈[-2,2]恒成立….
当x=0时,cos0=cos0=1.
不妨取x=1,则cos1
2=cos1,所以cos1≠cos
21…
所以假设不成立,在集合M上,
函数f(x)与g(x)不是互为“H函数”….
(3)解:由题意得,a
x+1=a
x+1(a>0且a≠1)…
变形得,a
x(a-1)=1,
由于a>0且a≠1

,
因为a
x>0,所以
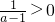
,即a>1…
此时x=-log
a(a-1),
集合M={x|x=-log
a(a-1),a>1}…
分析:(1)由f(x)=ax+b,g(x)=mx+n,f(x)与g(x)互为“H函数”,知f(g(x))=g(f(x))成立.即ag(x)+b=mf(x)+n恒成立,由此能够证明f(n)=g(b).
(2)假设函数f(x)与g(x)互为“H函数”,则对于任意的x∈M,f(g(x))=g(f(x))恒成立.即cosx
2=cos
2x,对于任意x∈[-2,2]恒成立,由此能推导出在集合M上,函数f(x)与g(x)不是互为“H函数”.
(3)由题意得,a
x+1=a
x+1(a>0且a≠1),变形得a
x(a-1)=1,由于a>0且a≠1

,由此能求出a的取值范围及集合M.
点评:本题考查函数值相等的证明,考查两个函数是否互为“H函数”的判断,考查满足条件的实数的取值范围的求法,解题时要认真审题,注意等价转化思想的合理运用.

 ,
,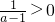 ,即a>1…
,即a>1… ,由此能求出a的取值范围及集合M.
,由此能求出a的取值范围及集合M.
