
分析 (1)利用(|a|+|b|)2≤2(a2+b2)即可证明.
(2)由(1)中|a|+|b|≤1,自然联想|a|-|b|≤|a±b|≤|a|+|b|,而a、b是方程的系数,欲证根的绝对值小于等于1,由韦达定理,寻找解题途径.
解答 证明:(1)∵a2+b2=$\frac{1}{2}$,
∴(|a|+|b|)2≤2(a2+b2)=1,当且仅当a=b时取等号.
∴|a|+|b|≤1;
(2)设方程的两根为x1、x2,由韦达定理得x1+x2=-a,x1x2=b,
代入|a|+|b|≤1有|x1+x2|+|x1x2|≤1(*).
①用|x1|-|x2|≤|x1+x2|,把(*)式放缩得|x1|-|x2|+|x1x2|≤1,
∴(|x1|-1)(|x2|+1)≤0,∵|x2|+1>0,∴|x1|≤1.
②用|x2|-|x1|≤|x1+x2|,把(*)式放缩,
同理可得,|x2|≤1.综合①②有|x1|≤1,|x2|≤1.
故方程x2+ax+b=0的两根的绝对值均小于1.
点评 本题考查了基本不等式的性质,考查放缩法的运用,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
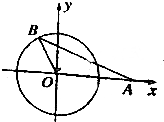 如图所示,圆O的圆心为坐标原点,B为圆O上一点,若点A坐标为(3,0),|AB|=4,sin∠AOB=$\frac{\sqrt{15}}{4}$.
如图所示,圆O的圆心为坐标原点,B为圆O上一点,若点A坐标为(3,0),|AB|=4,sin∠AOB=$\frac{\sqrt{15}}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
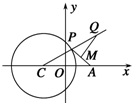 如图所示,已知C为圆${({x+\sqrt{2}})^2}$+y2=4的圆心,点A(${\sqrt{2}$,0),P是圆上的动点,点Q在圆的半径CP所在直线上,且$\overrightarrow{MQ}$•$\overrightarrow{AP}$=0,$\overrightarrow{AP}$=2$\overrightarrow{AM}$.当点P在圆上运动时,则点Q的轨迹方程为x2-y2=1.
如图所示,已知C为圆${({x+\sqrt{2}})^2}$+y2=4的圆心,点A(${\sqrt{2}$,0),P是圆上的动点,点Q在圆的半径CP所在直线上,且$\overrightarrow{MQ}$•$\overrightarrow{AP}$=0,$\overrightarrow{AP}$=2$\overrightarrow{AM}$.当点P在圆上运动时,则点Q的轨迹方程为x2-y2=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com