Question

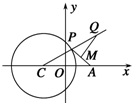
16．如图所示，已知C为圆${（{x+\sqrt{2}}）^2}$+y²=4的圆心，点A（${\sqrt{2}$，0），P是圆上的动点，点Q在圆的半径CP所在直线上，且$\overrightarrow{MQ}$•$\overrightarrow{AP}$=0，$\overrightarrow{AP}$=2$\overrightarrow{AM}$．当点P在圆上运动时，则点Q的轨迹方程为x²-y²=1．

Answer 1

分析 由题意可得QM是线段PA的垂直平分线，PC=QC-QA=2，可得点Q的轨迹是以C（-$\sqrt{2}$，0），A（$\sqrt{2}$，0）为焦点，长轴长为2的双曲线，由此能求出点Q的轨迹方程．

解答 解：由题意可得C（-$\sqrt{2}$，0），圆C的半径为2，M为线段AP的中点，且QM⊥AP，即QM是线段PA的垂直平分线，
故有QP=QA．
∵PC=2，故有PC=QC-QP=QC-QA=2，故点Q在以C、A为焦点的双曲线上，
且2a=1，∴a=1，又c=$\sqrt{2}$，∴b=$\sqrt{{c}^{2}{-a}^{2}}$=1．
设点Q的坐标为（x，y），则双曲线的方程为 $\frac{{x}^{2}}{1}$-$\frac{{y}^{2}}{{1}^{2}}$=1，即 x²-y²=1，
故答案为：x²-y²=1．

点评 本题考查点的轨迹方程的求法，解题时要认真审题，注意椭圆、圆的简单性质的合理运用，属于中档题．