
分析 (1)由题意求出圆心(0,0)到直线l1:x-y-2$\sqrt{2}$=0的距离,可得圆的半径长,得到圆的方程,连接OG,OM,由题意知|OG|=$\sqrt{{1}^{2}+{3}^{2}}=\sqrt{10}$,|GM|=$\sqrt{O{G}^{2}-O{M}^{2}}=\sqrt{6}$,从而求得以G为圆心,|GM|为半径的圆的方程为(x-1)2+(y-3)2=6,再利用圆系方程可得直线MN的方程是x+3y-4=0;
(2)直线l1的斜率为1,且l⊥l1,可得直线l的斜率为-1,设直线l的方程为y=-x+b,联立圆的方程与直线方程,化为关于x的一元二次方程,利用根与系数的关系可得P,Q两点横坐标的和与积,结合∠POQ为钝角,得$\overrightarrow{OP}•\overrightarrow{OQ}$<0,即x1x2+y1y2<0,从而可得直线l的纵截距的取值范围.
解答 解:(1)由题意得,圆心(0,0)到直线l1:x-y-2$\sqrt{2}$=0的距离为圆的半径长r,
即$r=\frac{|0-0-2\sqrt{2}|}{\sqrt{2}}=2$,
∴圆C的标准方程为x2+y2=4.
连接OG,OM,由题意知|OG|=$\sqrt{{1}^{2}+{3}^{2}}=\sqrt{10}$,|GM|=$\sqrt{O{G}^{2}-O{M}^{2}}=\sqrt{6}$,
∴以G为圆心,|GM|为半径的圆的方程为(x-1)2+(y-3)2=6 ①,
又圆C的方程为x2+y2=4 ②,
由①-②得直线MN的方程是x+3y-4=0;
(2)∵直线l1的斜率为1,且l⊥l1,∴直线l的斜率为-1,设直线l的方程为y=-x+b,
则与圆C的方程x2+y2=4 联立,化简得2x2-2bx+b2-4=0.
设P(x1,y1),Q(x2,y2),则x1,x2是方程2x2-2bx+b2-4=0的两个不同的根,
故x1+x2=b,${x}_{1}{x}_{2}=\frac{{b}^{2}-4}{2}$ ③,
由△=(-2b)2-8(b2-4)>0,得-2$\sqrt{2}$<b<$2\sqrt{2}$.
∵∠POQ为钝角,∴$\overrightarrow{OP}•\overrightarrow{OQ}$<0,即x1x2+y1y2<0,
又y1=-x1+b,y2=-x2+b,
∴${x}_{1}{x}_{2}+{y}_{1}{y}_{2}=2{x}_{1}{x}_{2}-b({x}_{1}+{x}_{2})+{b}^{2}$<0 ④,
由③④得b2<4,即-2<b<2,满足△>0.
当$\overrightarrow{OP}$与$\overrightarrow{OQ}$反向共线时,直线y=-x+b过原点,此时b=0,不符合题意,
故直线l的纵截距的取值范围是-2<b<2,且b≠0.
点评 本题考查直线与圆的位置关系的应用,训练了利用圆系方程求两圆公共弦所在的直线方程,考查了平面向量的数量积运算,是中档题.


科目:高中数学 来源: 题型:解答题
 如图所示,△ABC与△DBC是边长均为2的等边三角形,且所在两平面互相垂直,EA⊥平面ABC,且EA=$\sqrt{3}$.
如图所示,△ABC与△DBC是边长均为2的等边三角形,且所在两平面互相垂直,EA⊥平面ABC,且EA=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
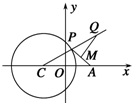 如图所示,已知C为圆${({x+\sqrt{2}})^2}$+y2=4的圆心,点A(${\sqrt{2}$,0),P是圆上的动点,点Q在圆的半径CP所在直线上,且$\overrightarrow{MQ}$•$\overrightarrow{AP}$=0,$\overrightarrow{AP}$=2$\overrightarrow{AM}$.当点P在圆上运动时,则点Q的轨迹方程为x2-y2=1.
如图所示,已知C为圆${({x+\sqrt{2}})^2}$+y2=4的圆心,点A(${\sqrt{2}$,0),P是圆上的动点,点Q在圆的半径CP所在直线上,且$\overrightarrow{MQ}$•$\overrightarrow{AP}$=0,$\overrightarrow{AP}$=2$\overrightarrow{AM}$.当点P在圆上运动时,则点Q的轨迹方程为x2-y2=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 49,9 | B. | 7,3 | C. | $\sqrt{7}$,$\sqrt{3}$ | D. | 7,$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
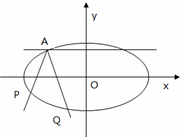 如图为焦点在x轴上的椭圆,且离心率e=$\frac{\sqrt{2}}{2}$,且过点A(-2,1),有椭圆上异于点A的点P出发的光线射到点A处被直线y=1反射后交椭圆于点Q(点Q与点P不重合).
如图为焦点在x轴上的椭圆,且离心率e=$\frac{\sqrt{2}}{2}$,且过点A(-2,1),有椭圆上异于点A的点P出发的光线射到点A处被直线y=1反射后交椭圆于点Q(点Q与点P不重合).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com