
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:高中数学 来源:不详 题型:单选题
| A.(2k-9 ,2 k-8] | B.(2 k-8 -1, 2k-9-1] | C.(28-k -1, 29-k-1] | D.(27-k -1, 28-k-1] |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
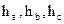 是三角形
是三角形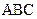 三条边上的高.P为三角形内任一点,P到相应三边的距离分别为
三条边上的高.P为三角形内任一点,P到相应三边的距离分别为 ,我们可以得到结论:
,我们可以得到结论: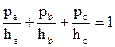
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
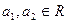 且
且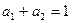 ,求证
,求证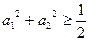
 函数
函数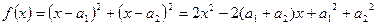 因为对一切
因为对一切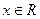 ,恒有
,恒有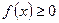 ,所以
,所以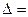 4-8
4-8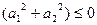 ,从而
,从而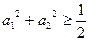
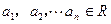 ,且
,且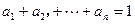 ,请写出上述结论的推广式;
,请写出上述结论的推广式;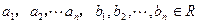 ,求证
,求证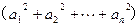
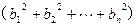
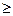
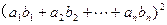 .[
.[查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com