
| A.(2k-9 ,2 k-8] | B.(2 k-8 -1, 2k-9-1] | C.(28-k -1, 29-k-1] | D.(27-k -1, 28-k-1] |
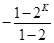 =2kx0-2k+1,再由题设条件xn-1≤257,则xn=f(xn-1),否则停止赋值,可得到2kx0-2k+1>257,且2k-1x0-2k-1+1≤257,解此二不等式即可得到x0的取值范围选出正确选项.
=2kx0-2k+1,再由题设条件xn-1≤257,则xn=f(xn-1),否则停止赋值,可得到2kx0-2k+1>257,且2k-1x0-2k-1+1≤257,解此二不等式即可得到x0的取值范围选出正确选项. =2kx0-2k+1;
=2kx0-2k+1;

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
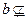 平面
平面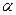 ,直线
,直线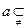 平面
平面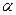 ,直线
,直线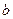 ∥平面
∥平面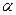 ,则直线
,则直线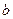 ∥直线
∥直线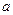 ”的结论显然是错误的,这是因为
”的结论显然是错误的,这是因为 查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.正方形的对角线相等 | B.矩形的对角线相等 | C.正方形是矩形 | D.其 他 他 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com