
已知函数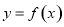 的图象与
的图象与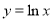 的图象关于直线
的图象关于直线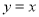 对称,则
对称,则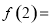 ( )
( )
A.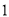 B.
B.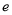 C.
C.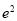 D.
D.
科目:高中数学 来源:2013-2014学年广东省广州市毕业班综合测试二理科数学试卷(解析版) 题型:填空题
已知四边形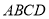 是边长为
是边长为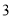 的正方形,若
的正方形,若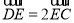 ,
,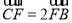 ,则
,则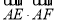 的值为.
的值为.
已知四边形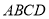 是边长为
是边长为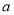 的正方形,若
的正方形,若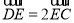 ,
,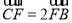 ,则
,则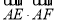 的值为.
的值为.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省东莞市高三第二次模拟考试文科数学试卷(解析版) 题型:解答题
已知函数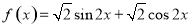 ,
,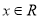 .
.
(1)求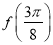 的值;
的值;
(2)求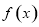 的最大值和最小正周期;
的最大值和最小正周期;
(3)若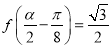 ,
,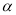 是第二象限的角,求
是第二象限的角,求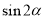 .
.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省东莞市高三第二次模拟考试文科数学试卷(解析版) 题型:选择题
若 ,则点
,则点 必在( )
必在( )
A.直线 的左下方
的左下方
B.直线 的右上方
的右上方
C.直线 的右上方
的右上方
D.直线 的左下方
的左下方
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省东莞市高三模拟(一)理科数学试卷(解析版) 题型:解答题
已知函数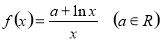 .
.
(1)若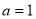 ,求曲线
,求曲线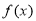 在点
在点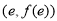 处的切线方程;
处的切线方程;
(2)求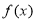 的极值;
的极值;
(3)若函数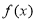 的图象与函数
的图象与函数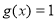 的图象在区间
的图象在区间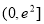 上有公共点,求实数
上有公共点,求实数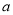 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省东莞市高三模拟(一)理科数学试卷(解析版) 题型:填空题
请阅读下列材料:若两个正实数a1,a2满足 ,那么
,那么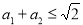 .
.
证明:构造函数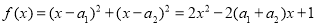 ,因为对一切实数x,恒有
,因为对一切实数x,恒有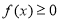 ,所以
,所以 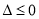 ,从而得
,从而得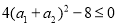 ,所以
,所以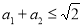 .
.
根据上述证明方法,若n个正实数满足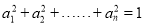 时,你能得到的结论为 .(不必证明)
时,你能得到的结论为 .(不必证明)
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省东莞市高三模拟(一)文科数学试卷(解析版) 题型:解答题
对某电子元件进行寿命追踪调查,所得情况如右频率分布直方图.
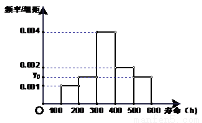
(1)图中纵坐标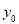 处刻度不清,根据图表所提供的数据还原
处刻度不清,根据图表所提供的数据还原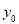 ;
;
(2)根据图表的数据按分层抽样,抽取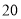 个元件,寿命为
个元件,寿命为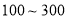 之间的应抽取几个;
之间的应抽取几个;
(3)从(2)中抽出的寿命落在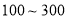 之间的元件中任取
之间的元件中任取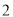 个元件,求事件“恰好有一个寿命为
个元件,求事件“恰好有一个寿命为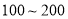 ,一个寿命为
,一个寿命为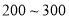 ”的概率.
”的概率.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年山东省青岛市高三4月统一质量检测考试文科数学试卷(解析版) 题型:解答题
如图,在四棱锥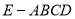 中,底面
中,底面 为正方形,
为正方形,
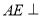 平面
平面 ,已知
,已知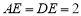 ,
,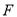 为线段
为线段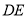 的中点.
的中点.
(1)求证: 平面
平面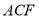 ;
;
(2)求四棱锥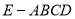 的体积.
的体积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com