(1)已知圆C经过A(5,1),B(1,3)两点,圆心在x轴上,求圆C的方程.
(2)求与圆x2+y2-2x+4y+1=0同心,且与直线2x-y+1=0相切的圆的方程.
解:(1)∵A(5,1),B(1,3),
∴线段AB的中点坐标为(
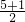
,
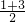
),即(3,2),
直线AB的斜率k
AB=
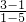
=-

,
∴线段AB垂直平分线的方程为y-2=2(x-3),即y=2x-4,
又圆心在x轴上,∴令y=0,得到2x-4=0,即x=2,
∴圆心C坐标为(2,0),
∴圆的半径r=|AC|=
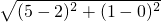
=

,
则圆C的方程为(x-2)
2+y
2=10.
(2)解:所求圆的圆心坐标为 (1,-2),
因为直线与圆相切,所以圆的半径为:
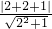
=

所以所求圆的方程为:(x-1)
2+(y+2)
2=5.
分析:(1)根据垂径定理可得弦AB的垂直平分线必然过圆心,故利用线段中点坐标公式求出AB的中点坐标,由A和B的坐标求出直线AB的斜率,根据两直线垂直时斜率的乘积为-1求出线段AB垂直平分线的斜率,由求出的斜率与AB的中点坐标得出线段AB的垂直平分线方程,又圆心在x轴上,令求出的直线方程中y=0,求出x的值,可确定出圆心C的坐标,再由A和C的坐标,利用两点间的距离公式求出|AC|的长,即为圆C的半径,由圆心和半径写出圆C的标准方程即可.
(2)求出圆的圆心坐标,利用圆与直线相切,求出圆的半径,即可得到圆的方程.
点评:此题考查了圆的标准方程,涉及的知识有:线段的中点坐标公式,两直线垂直时斜率满足的关系,直线的点斜式方程,一次函数与坐标轴的交点,两点间的距离公式,以及垂径定理的运用,根据题意确定出圆心C的坐标是解本题的关键,考查直线与圆相切的关系的应用,圆的方程的求法,考查计算能力.

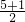 ,
,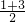 ),即(3,2),
),即(3,2),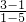 =-
=- ,
,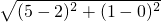 =
= ,
,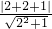 =
=

