
已知函数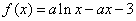 (
(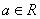 ).
).
(Ⅰ) 讨论函数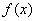 的单调性;
的单调性;
(Ⅱ)若函数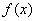 的图像在点
的图像在点 处的切线的倾斜角为
处的切线的倾斜角为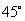 ,且函数
,且函数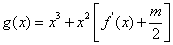 在区间
在区间 上不单调,求
上不单调,求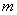 的取值范围;
的取值范围;
(Ⅲ)试比较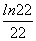 +
+ +…+
+…+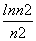 与
与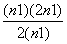 的大小(n∈N+,且n≥2),并证明你的结论.
的大小(n∈N+,且n≥2),并证明你的结论.
解:(Ⅰ)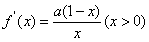 …………1分
…………1分
当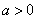 时,
时,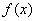 的单调增区间为
的单调增区间为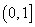 ,单调减区间为
,单调减区间为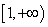 ; …
; … ………2分
………2分
当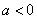 时,
时,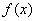 的单调增区间为
的单调增区间为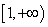 ,单调减区间为
,单调减区间为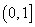 …………3分
…………3分
当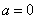 时,
时,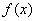 不是单调函数。 …………4分
不是单调函数。 …………4分
(Ⅱ)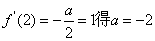 ,
,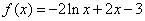
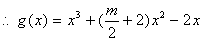 ,
,
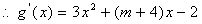 …………5分
…………5分
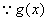 在区间
在区间 上不单调,且
上不单调,且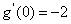
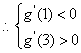 …………7分
…………7分
解得 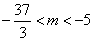
 …………8分
…………8分
(Ⅲ)结论: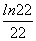 +
+ +…+
+…+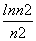 <
<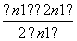 (n∈N+且n≥2). …………
(n∈N+且n≥2). ………… 9分
9分
证明如下:令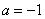 此时
此时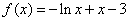 ,所以
,所以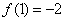
由(Ⅰ)知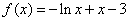 在
在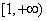 上单调递增,
上单调递增,
所以当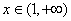 时,
时,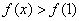 ,
,
即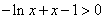 ,
,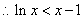 对一切
对一切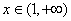 成立, …………11分
成立, …………11分
则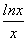 <1-
<1-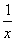 对一切
对一切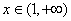 也成立,
也成立,
所以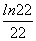 +
+ +…+
+…+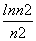 <1-
<1-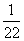 +1-
+1-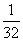 +…+1-
+…+1-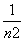
=n-1-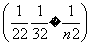 <n-1-
<n-1-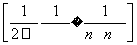 …………13分
…………13分
=n-1-
=n-1-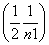 =
=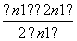 (n∈N*且n≥2). ………… 14分
(n∈N*且n≥2). ………… 14分
另解:也可先证明 对一切
对一切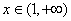 成立,证法可通过令
成立,证法可通过令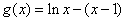 ,再求导研究单调性进行证明.
,再求导研究单调性进行证明.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:高中数学 来源: 题型:
已知椭圆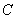 :
: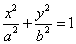
 的两个焦点分别为
的两个焦点分别为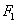 ,
, ,离心率为
,离心率为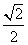 ,且过点
,且过点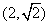 .
.
(Ⅰ)求椭圆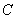 的标准方程;
的标准方程;
(Ⅱ) ,
,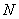 ,
,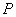 ,
,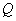 是椭圆
是椭圆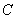 上的四个不同的点,两条都不和
上的四个不同的点,两条都不和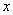 轴垂直的直线
轴垂直的直线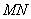 和
和 分别过点
分别过点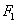 ,
, ,且这两条直线互相垂直,求证:
,且这两条直线互相垂直,求证: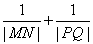 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com