
【题目】在△ABC中,角A,B,C的对边为a,b,c,角A,B,C的大小成等差数列,向量 ![]() =(sin
=(sin ![]() ,cos
,cos ![]() ),=(cos
),=(cos ![]() ,﹣
,﹣ ![]() cos
cos ![]() ),f(A)=
),f(A)= ![]()
![]() ,
,
(1)若f(A)=﹣ ![]() ,试判断三角形ABC的形状;
,试判断三角形ABC的形状;
(2)若b= ![]() ,a=
,a= ![]() ,求边c及S△ABC .
,求边c及S△ABC .
【答案】
(1)解:∵A,B,C成等差数列,可得:2B=A+C,
又∵A+B+C=180°,
∴B=60°.
∵向量 ![]() =(sin
=(sin ![]() ,cos
,cos ![]() ),
), ![]() =(cos
=(cos ![]() ,﹣
,﹣ ![]() cos
cos ![]() ),f(A)=
),f(A)= ![]()
![]() =﹣
=﹣ ![]() ,
,
∴f(A)= ![]()
![]() =sin
=sin ![]() cos
cos ![]() ﹣
﹣ ![]() cos
cos ![]() cos
cos ![]() =
= ![]() sinA﹣
sinA﹣ ![]() cosA﹣
cosA﹣ ![]() =sin(A﹣60°)﹣
=sin(A﹣60°)﹣ ![]() =﹣
=﹣ ![]() ,
,
∴可得:sin(A﹣60°)=0.
∵A∈(0,60°],可得:A﹣60°∈(﹣60°,0],
∴可得:A=60°,即A=B=C=60°.
∴三角形ABC的形状为:正三角形
(2)解:∵B=60°,b= ![]() ,a=
,a= ![]() ,
,
∴由余弦定理b2=a2+c2﹣2accosB,可得:3=2+c2﹣2× ![]() ,整理可得:c2﹣
,整理可得:c2﹣ ![]() ﹣1=0,
﹣1=0,
∴解得:c= ![]() ,或
,或 ![]() (舍去),
(舍去),
∴S△ABC= ![]() acsinB=
acsinB= ![]()
![]() ×
× ![]() =
= ![]()
【解析】(1)利用已知及等差数列的性质,三角形内角和定理可求B=60°,利用数量积的运算及三角函数恒等变换的应用可求sin(A﹣60°)=0,结合A的范围可求A=60°,即可得解.(2)利用已知及余弦定理可求c,进而利用三角形面积公式即可计算得解.
【考点精析】根据题目的已知条件,利用余弦定理的定义的相关知识可以得到问题的答案,需要掌握余弦定理:![]() ;
;![]() ;
;![]() .
.


科目:高中数学 来源: 题型:
【题目】在无重复数字的五位数a1a2a3a4a5中,若a1<a2 , a2>a3 , a3<a4 , a4>a5时称为波形数,如89674就是一个波形数,由1,2,3,4,5组成一个没有重复数字的五位数是波形数的概率是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}是等差数列,{bn}是各项均为正数的等比数列,满足a1=b1=1,b2﹣a3=2b3 , a3﹣2b2=﹣1
(1)求数列{an}和{bn}的通项公式
(2)设cn=an+bn , n∈N* , 求数列{cn}的前n项和Sn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高校学生总数为8000人,其中一年级1600人,二年级3200人,三年级2000人,四年级1200人.为了完成一项调查,决定采用分层抽样的方法,从中抽取容量为400的样本.
(1)各个年级分别抽取了多少人?
(2)若高校教职工有505人,需要抽取50个样本,你会采用哪种抽样方法,请写出具体抽样过程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数 ![]() 的图象,只需把y=3sin2x上的所有的点( )
的图象,只需把y=3sin2x上的所有的点( )
A.向左平行移动 ![]() 长度单位
长度单位
B.向右平行移动 ![]() 长度单位
长度单位
C.向右平行移动 ![]() 长度单位
长度单位
D.向左平行移动 ![]() 长度单位
长度单位
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某地一天从6时到14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b.
(1)求这一天的最大温差;
(2)写出这段曲线的函数解析式.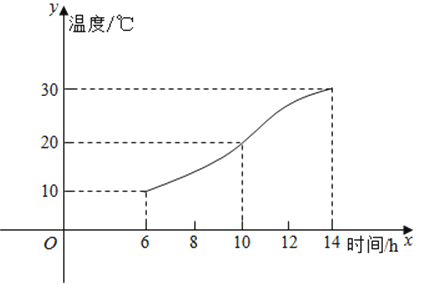
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com