
【题目】如图,有一直径为8米的半圆形空地,现计划种植甲、乙两种水果,已知单位面积种植甲水果的经济价值是种植乙水果经济价值的5倍,但种植甲水果需要有辅助光照.半圆周上的![]() 处恰有一可旋转光源满足甲水果生长的需要,该光源照射范围是
处恰有一可旋转光源满足甲水果生长的需要,该光源照射范围是![]() ,点
,点![]() 在直径
在直径![]() 上,且
上,且![]() .
.

(1)若![]() 米,求
米,求![]() 的长;
的长;
(2)设![]() , 求该空地产生最大经济价值时种植甲种水果的面积.
, 求该空地产生最大经济价值时种植甲种水果的面积.
科目:高中数学 来源: 题型:
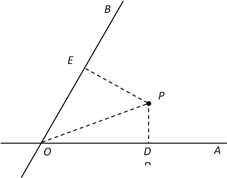
【题目】如图,![]() 、
、![]() 是两条公路(近似看成两条直线),
是两条公路(近似看成两条直线),![]() ,在
,在![]() 内有一纪念塔
内有一纪念塔![]() (大小忽略不计),已知
(大小忽略不计),已知![]() 到直线
到直线![]() 、
、![]() 的距离分别为
的距离分别为![]() 、
、![]() ,
,![]() =6千米,
=6千米,![]() =12千米.现经过纪念塔
=12千米.现经过纪念塔![]() 修建一条直线型小路,与两条公路
修建一条直线型小路,与两条公路![]() 、
、![]() 分别交于点
分别交于点![]() 、
、![]() .
.
(1)求纪念塔![]() 到两条公路交点
到两条公路交点![]() 处的距离;
处的距离;
(2)若纪念塔![]() 为小路
为小路![]() 的中点,求小路
的中点,求小路![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为增强市民的节能环保意识,郑州市面向全市征召义务宣传志愿者,从符合条件的500名志愿者中随机抽取100名,其年龄频率分布直方图如图所示,其中年龄分组区是:![]() .
.
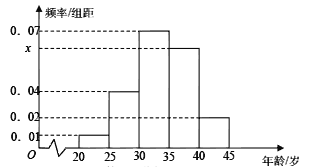
(Ⅰ)求图中![]() 的值,并根据频率分布直方图估计这500名志愿者中年龄在
的值,并根据频率分布直方图估计这500名志愿者中年龄在![]() 岁的人数;
岁的人数;
(Ⅱ)在抽出的100名志愿者中按年龄采用分层抽样的方法抽取10名参加中心广场的宣传活动,再从这10名志愿者中选取3名担任主要负责人.记这3名志愿者中“年龄低于35岁”的人数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市![]() 户居民的月平均用电量(单位:度),以
户居民的月平均用电量(单位:度),以![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分组的频率分布直方图如图.
分组的频率分布直方图如图.
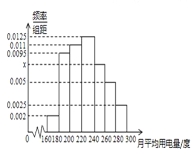
(I)求直方图中![]() 的值;
的值;
(II)求月平均用电量的众数和中位数;
(III)在月平均用电量为![]() ,
,![]() ,
,![]() ,
,![]() 的四组用户中,用分层抽样的方法抽取
的四组用户中,用分层抽样的方法抽取![]() 户居民,则月平均用电量在
户居民,则月平均用电量在![]() 的用户中应抽取多少户?
的用户中应抽取多少户?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50m/min.在甲出发2min后,乙从A乘缆车到B,在B处停留1min后,再从B匀速步行到C.假设缆车匀速直线运动的速度为130m/min,山路AC长为1260m,经测量,![]() ,
,![]() .
.
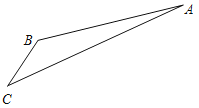
(Ⅰ)问乙出发多少分钟后,乙在缆车上与甲的距离最短?
(Ⅱ)为使两位游客在![]() 处互相等待的时间不超过
处互相等待的时间不超过![]() 分钟,乙步行的速度应控制在什么范围内?
分钟,乙步行的速度应控制在什么范围内?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在边长为1的等边三角形ABC中,D,E分别是AB,AC边上的点,AD=AE,F是BC的中点,AF与DE交于点G,将△ABF沿AF折起,得到如图2所示的三棱锥A﹣BCF,其中BC=![]() .
.
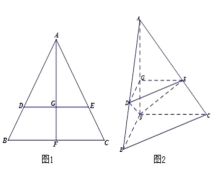
(Ⅰ)证明:DE∥平面BCF;
(Ⅱ)证明:CF⊥平面ABF;
(Ⅲ)当AD=![]() 时,求三棱锥F﹣DEG的体积.
时,求三棱锥F﹣DEG的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知国家某5A级大型景区对拥挤等级与每日游客数量![]() (单位:百人)的关系有如下规定:当
(单位:百人)的关系有如下规定:当![]()
![]() 时,拥挤等级为“优”;当
时,拥挤等级为“优”;当![]()
![]() 时,拥挤等级为“良”;当
时,拥挤等级为“良”;当![]()
![]() 时,拥挤等级为“拥挤”;当
时,拥挤等级为“拥挤”;当![]()
![]() 时,拥挤等级为“严重拥挤”。该景区对6月份的游客数量作出如图的统计数据:
时,拥挤等级为“严重拥挤”。该景区对6月份的游客数量作出如图的统计数据:
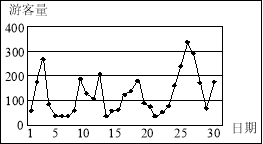
(Ⅰ)下面是根据统计数据得到的频率分布表,求出![]() 的值,并估计该景区6月份游客人数的平均值(同一组中的数据用该组区间的中点值作代表);
的值,并估计该景区6月份游客人数的平均值(同一组中的数据用该组区间的中点值作代表);
游客数量 (单位:百人) |
|
|
|
|
天数 |
|
|
|
|
频率 |
|
|
|
|
(Ⅱ)某人选择在6月1日至6月5日这5天中任选2天到该景区游玩,求他这2天遇到的游客拥挤等级均为“优”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数);在以原点
为参数);在以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(I)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(II)若射线![]() 与曲线
与曲线![]() ,
,![]() 的交点分别为
的交点分别为![]() (
(![]() 异于原点),当斜率
异于原点),当斜率![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com