
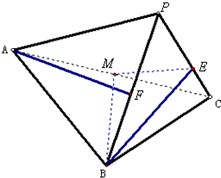
 在三棱锥P-ABC中,F,M分别是棱PB,AC的中点,E为PC上一动点.
在三棱锥P-ABC中,F,M分别是棱PB,AC的中点,E为PC上一动点.分析 (1)当E为PC上靠近C的三等分点时,取PE中点G,则E为CG中点,连结FG、AG,推导出平面AGF∥平面MEB,从而得到AF∥平面MEB.
(2)由M是PC中点,得$S△BMC=\frac{1}{2}{S}_{△ABC}$,由E为PC上靠近C的三等分点,设点P到平面ABC的距离为h,则E到平面BMC的距离为$\frac{1}{3}h$,由此能求出三棱锥C-MEB与三棱锥C-PAB的体积比.
解答 解:(1)当E为PC上靠近C的三等分点时,AF∥平面MEB.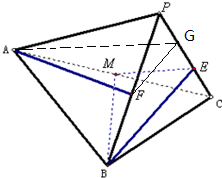
证明:取PE中点G,则E为CG中点,
连结FG、AG,
∵F,M分别是棱PB,AC的中点,G为PE中点,E为CG中点,
∴GF∥BE,ME∥AG,
∵AG∩FG=G,ME∩BE=E,
AG、FG?平面AGF,ME、BE?平面MEB,
∴平面AGF∥平面MEB,
∵AF?平面AGF,∴AF∥平面MEB.
(2)∵M是PC中点,∴$S△BMC=\frac{1}{2}{S}_{△ABC}$,
∵E为PC上靠近C的三等分点,
设点P到平面ABC的距离为h,
∴E到平面BMC的距离为$\frac{1}{3}h$,
∴三棱锥C-MEB与三棱锥C-PAB的体积比:
$\frac{{V}_{C-MEB}}{{V}_{C-PAB}}$=$\frac{{V}_{E-BMC}}{{V}_{P-ABC}}$=$\frac{\frac{1}{3}×{S}_{△BMC}×\frac{1}{3}h}{\frac{1}{3}×{S}_{△ABC}×h}$=$\frac{1}{6}$.
∴三棱锥C-MEB与三棱锥C-PAB的体积比为$\frac{1}{6}$.
点评 本题考查满足线面平行的点的位置的确定,考查两个三棱锥的体积之比的求法,是中档题,解题时要认真审题,注意空间思维能力的培养产.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某正三棱柱(底面是正三角形的直棱柱)的正视图和俯视图如图所示.若它的体积为2$\sqrt{3}$,则它的侧视图面积为( )
某正三棱柱(底面是正三角形的直棱柱)的正视图和俯视图如图所示.若它的体积为2$\sqrt{3}$,则它的侧视图面积为( )| A. | 2$\sqrt{3}$ | B. | 3 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | $\sqrt{5}-2$ | C. | $\sqrt{5}+2$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com