
【题目】已知向量 ![]() =(
=( ![]() sin
sin ![]() ,1),
,1), ![]() =(cos
=(cos ![]() ,cos2
,cos2 ![]() ),f(x)=
),f(x)= ![]()
![]() .
.
(1)求函数f(x)的解析式及其单调递增区间;
(2)将f(x)的图象向右平移 ![]() 个单位长度得到g(x)的图象,若g(x)﹣k≤0在区间[0,
个单位长度得到g(x)的图象,若g(x)﹣k≤0在区间[0, ![]() ]上恒成立,求实数k的取值范围.
]上恒成立,求实数k的取值范围.
【答案】
(1)解:由题意得,f(x)= ![]()
![]() =
= ![]() sin
sin ![]() cos
cos ![]() +cos2
+cos2 ![]()
= ![]() sin
sin ![]() +
+ ![]() cos
cos ![]() +
+ ![]() =
= ![]() ,
,
由 ![]() 得,
得,
![]() ,
,
∴函数f(x)的单调递增区间是 ![]()
(2)解:将f(x)的图象向右平移 ![]() 个单位长度得到g(x)=
个单位长度得到g(x)= ![]() 的图象,
的图象,
当 ![]() 时,
时, ![]() ,∴
,∴ ![]() ,
,
∴ ![]() ,
,
∵g(x)﹣k≤0在区间[0, ![]() ]上恒成立,
]上恒成立,
∴k≥g(x)max= ![]() ,
,
∴实数k的取值范围是[ ![]() ,+∞).
,+∞).
【解析】(1)利用向量的数量积运算、二倍角公式,两角和的正弦公式化简解析式,由正弦函数的增区间求出f(x)单调递增区间;(2)由三角函数图象的平移法则求出g(x),由由x的范围和正弦函数的性质求出g(x)的值域,由条件和恒成立问题转化为求最值,从而求出实数k的取值范围.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】已知数列![]() ),若
),若![]() 为等比数列,则称
为等比数列,则称![]() 具有性质
具有性质![]() .
.
(1)若数列![]() 具有性质
具有性质![]() ,且
,且![]() ,求
,求![]() 、
、![]() 的值;
的值;
(2)若![]() ,求证:数列
,求证:数列![]() 具有性质
具有性质![]() ;
;
(3)设![]() ,数列
,数列![]() 具有性质
具有性质![]() ,其中
,其中![]() ,若
,若![]() ,求正整数
,求正整数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥O﹣ABCD中,底面ABCD是边长为1的正方形,OA⊥底面ABCD,OA=2,M为OA中点.
(1)求证:直线BD⊥平面OAC;
(2)求直线MD与平面OAC所成角的大小;
(3)求点A到平面OBD的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的顶点A(5,1),AB边上的中线CM所在直线方程为2x﹣y﹣5=0,AC边上的高BH所在直线方程为x﹣2y﹣5=0.求:
(1)顶点C的坐标;
(2)直线BC的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A,ω,φ均为正的常数)的最小正周期为π,当x= ![]() 时,函数f(x)取得最小值,则下列结论正确的是( )
时,函数f(x)取得最小值,则下列结论正确的是( )
A.f(2)<f(﹣2)<f(0)
B.f(0)<f(2)<f(﹣2)
C.f(﹣2)<f(0)<f(2)
D.f(2)<f(0)<f(﹣2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:(x﹣1)2+(y﹣2)2=25,直线l:(2m+1)x+(m+1)y﹣7m﹣4=0(m∈R)
(1)证明:直线l恒过定点,并判断直线l与圆的位置关系;
(2)当直线l被圆C截得的弦长最短时,求直线l的方程及最短弦的长度.
查看答案和解析>>
科目:高中数学 来源: 题型:
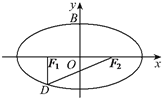
【题目】如图,设椭圆![]() (
(![]() )的左、右焦点分别为
)的左、右焦点分别为![]() ,点
,点![]() 在椭圆上,
在椭圆上, ![]() ,
, ![]() ,
, ![]() 的面积为
的面积为![]() .
.
(Ⅰ)求该椭圆的标准方程;
(Ⅱ)是否存在圆心在![]() 轴上的圆,使圆在
轴上的圆,使圆在![]() 轴的上方与椭圆
轴的上方与椭圆
有两个交点,且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点?若存在,求圆的方程,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() (0<φ<π,ω>0)为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为
(0<φ<π,ω>0)为偶函数,且函数y=f(x)图象的两相邻对称轴间的距离为 ![]() .
.
(1)求 ![]() 的值;
的值;
(2)将函数y=f(x)的图象向右平移 ![]() 个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
个单位后,再将得到的图象上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数y=g(x)的图象,求g(x)的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在“一带一路”的建设中,中石化集团获得了某地深海油田区块的开采权,集团在该地区随机初步勘探了几口井,取得了地质资料.进入全面勘探时期后,集团按网络点来布置井位进行全面勘探.由于勘探一口井的费用很高,如果新设计的井位与原有井位重合或接近,便利用旧井的地质资料,不必打这口新井,以节约勘探费用.勘探初期数据资料下表:

(1)在散点图中![]() 号旧井位置大致分布在一条直线附近,借助前5组数据求得回归线方程为
号旧井位置大致分布在一条直线附近,借助前5组数据求得回归线方程为![]() ,求
,求![]() ,并估计
,并估计![]() 的预报值;
的预报值;
(2)现准备勘探新井![]() ,若通过1、3、5、7号井计算出的
,若通过1、3、5、7号井计算出的![]() 的值(
的值(![]() 精确到0.01)相比于(1)中
精确到0.01)相比于(1)中![]() 的值之差(即:
的值之差(即:![]() )不超过10%,则使用位置最接近的已有旧井
)不超过10%,则使用位置最接近的已有旧井![]() ,否则在新位置打井,请判断可否使用旧井?(参考公式和计算结果:
,否则在新位置打井,请判断可否使用旧井?(参考公式和计算结果: ,
,![]() )
)
(3)设出油量与钻探深度的比值![]() 不低于20的勘探井称为优质井,在原有井号
不低于20的勘探井称为优质井,在原有井号![]() 的井中任意勘探3口井,求恰好2口是优质井的概率.
的井中任意勘探3口井,求恰好2口是优质井的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com