
 的离心率为e,焦点为F1、F2,抛物线C以F1为顶点,F2为焦点.设P为两条曲线的一个交点,若
的离心率为e,焦点为F1、F2,抛物线C以F1为顶点,F2为焦点.设P为两条曲线的一个交点,若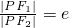 ,则e的值为
,则e的值为



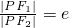 ?|PF1|=e|PF2|,所以|PF2|=d,
?|PF1|=e|PF2|,所以|PF2|=d, -c=2c,
-c=2c, .
.

 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:高中数学 来源: 题型:
A、
| ||||
B、
| ||||
C、
| ||||
| D、以上均不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,A,B是椭圆C:
如图,A,B是椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年威海市质检)(14分)如图,已知椭圆![]() 的离心率为e,点F为其下焦点,点A为其上顶点,过F的直线
的离心率为e,点F为其下焦点,点A为其上顶点,过F的直线![]() 与椭圆C相交于P、Q两点,且满足:
与椭圆C相交于P、Q两点,且满足:![]()
(1)试用a表示![]() ;
;
(2)求e的最大值;
(3)若![]() 取值范围;
取值范围;

查看答案和解析>>
科目:高中数学 来源:2010-2011学年山东省泰安市高三上学期期末考试数学理卷 题型:解答题
(本小题满分12分)
已知椭圆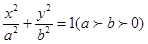 的离心率为e=
的离心率为e=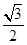 ,且过点(
,且过点(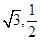 )
)
(Ⅰ)求椭圆的方程;
(Ⅱ)设直线l:y=kx+m(k≠0,m>0)与椭圆交于P,Q两点,且以PQ为对角线的菱形的一顶点为(-1,0),求:△OPQ面积的最大值及此时直线l的方程.
查看答案和解析>>
科目:高中数学 来源:2010年甘肃省高二第二阶段考试数学理卷 题型:选择题
已知椭圆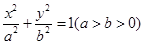 的离心率为e,焦点为F1、F2,抛物线C以F1为顶点,F2为焦点.设P为两条曲线的一个交点,若
的离心率为e,焦点为F1、F2,抛物线C以F1为顶点,F2为焦点.设P为两条曲线的一个交点,若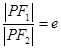 ,则e的值为( )
,则e的值为( )
A. 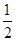 B.
B. 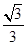 C.
C.
 D.
D.
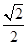
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com