
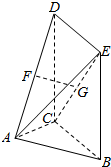
 如图,平面DCBE⊥平面ABC,四边形DCBE为矩形,且BC=$\sqrt{2}$AB=$\sqrt{2}$AC,F、G分别为AD、CE的中点.
如图,平面DCBE⊥平面ABC,四边形DCBE为矩形,且BC=$\sqrt{2}$AB=$\sqrt{2}$AC,F、G分别为AD、CE的中点.分析 (1)根据线面平行的判定定理进行证明FG∥平面ABC;
(2)根据面面垂直的判定定理即可证明平面ABE⊥平面ACD.
解答 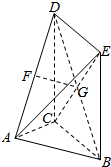 证明:(1)连接BD.因为四边形DCBE为矩形,且G为CE的中点,
证明:(1)连接BD.因为四边形DCBE为矩形,且G为CE的中点,
所以BD∩CE=G,且G为线段BD的中点.…(2分)
又因为F为AD的中点,所以FG为△DAB的中位线.
所以FG∥AB.…(4分)
又因为FG?平面ABC,AB?平面ABC,
所以FGP∥平面ABC.…(5分)
(2)因为DCBE为矩形,所以DC⊥CB.
又因为平面DCBE⊥平面ABC,
平面DCBE∩平面ABC=BC,DC?平面DCBE,
所以DC⊥平面ABC.…(7分)
所以DC⊥AB.…(8分)
因为BC=$\sqrt{2}$AB=$\sqrt{2}$AC,所以AB=AC,且AB2+AC2=BC2.
所以∠BAC=90°,即AB⊥AC.…(10分)
又因为AC∩DC=C,AC?平面ACD,DC?平面ACD,
所以AB⊥平面ACD.…(11分)
又AB?平面ABE,所以平面ABE⊥平面ACD.…12
点评 本题主要考查空间直线和平面平行和垂直的判定,利用相应的判定定理是解决本题的关键.


科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$f(2)<4f($\sqrt{2}$) | B. | $\sqrt{2}$f(2)>4f($\sqrt{2}$) | ||
| C. | $\sqrt{2}$f(2)=4f($\sqrt{2}$) | D. | 两者大小关系无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12π | B. | 16π | C. | $\frac{48π}{5}$ | D. | $\frac{144π}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 40小时 | B. | 50小时 | C. | 60小时 | D. | 80小时 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -6 | B. | -8 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com