
| A. | 40小时 | B. | 50小时 | C. | 60小时 | D. | 80小时 |
分析 由题意得$\left\{\begin{array}{l}{200={e}^{b}}\\{25={e}^{30k+b}}\end{array}\right.$,从而可得e30k=$\frac{1}{8}$,而e20k=$({e}^{30k})^{\frac{2}{3}}$,从而解得.
解答 解:由题意得,
$\left\{\begin{array}{l}{200={e}^{b}}\\{25={e}^{30k+b}}\end{array}\right.$,
故e30k=$\frac{25}{200}$=$\frac{1}{8}$,
故e20k+b=e20k•eb
=$(\frac{1}{8})^{\frac{2}{3}}$×200=50,
故选:B.
点评 本题考查了指数函数的变形应用及指数运算的应用.


 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
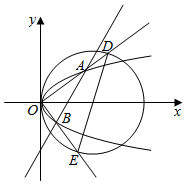 如图所示,过点(1,0)的直线与抛物线y2=x交于A、B两点,射线OA和OB分别和圆(x-2)2+y2=4交于D、E两点,若$\frac{{S}_{△OAB}}{{S}_{△ODE}}$=λ,则λ的最小值是( )
如图所示,过点(1,0)的直线与抛物线y2=x交于A、B两点,射线OA和OB分别和圆(x-2)2+y2=4交于D、E两点,若$\frac{{S}_{△OAB}}{{S}_{△ODE}}$=λ,则λ的最小值是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
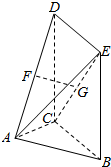 如图,平面DCBE⊥平面ABC,四边形DCBE为矩形,且BC=$\sqrt{2}$AB=$\sqrt{2}$AC,F、G分别为AD、CE的中点.
如图,平面DCBE⊥平面ABC,四边形DCBE为矩形,且BC=$\sqrt{2}$AB=$\sqrt{2}$AC,F、G分别为AD、CE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,2] | B. | [-1,2] | C. | (-∞,-1)∪(2,+∞) | D. | (-∞,-1]∪(2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
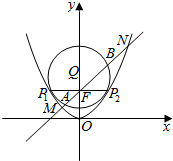 如图,抛物线C:x2=2py(p>0)的焦点为F(0,1),取垂直于y轴的直线与抛物线交于不同的两点P1,P2.过P1,P2作圆心为Q的圆,使抛物线的其余点均在圆外,且P1Q⊥P2Q.
如图,抛物线C:x2=2py(p>0)的焦点为F(0,1),取垂直于y轴的直线与抛物线交于不同的两点P1,P2.过P1,P2作圆心为Q的圆,使抛物线的其余点均在圆外,且P1Q⊥P2Q.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com