
分析 (Ⅰ)通过设数列{an}的公差为d,利用S1,S3,S9成等比数列可知(3+3d)2=9+36d,解出d的值,进而可得结论;
(Ⅱ)通过(I)可知,当an=1时Tn=n;当an=2n-1时,裂项、并项相加即得结论.
解答 解:(Ⅰ)设数列{an}的公差为d,则(3+3d)2=9+36d,
即d(d-2)=0,∴d=0或d=2,
当d=0时,an=1;
当d=2时,an=2n-1;
(Ⅱ)由(I)可知,当an=1时,Tn=n;
当an=2n-1时,Tn=$\frac{1}{1×3}$+$\frac{1}{3×5}$+…+$\frac{1}{(2n-1)(2n+1)}$
=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+…+$\frac{1}{2n-1}$-$\frac{1}{2n+1}$)
=$\frac{1}{2}$(1-$\frac{1}{2n+1}$)
=$\frac{n}{2n+1}$.
点评 本题考查数列的通项及前n项和,考查裂项相消法,考查分类讨论的思想,考查运算求解能力,注意解题方法的积累,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
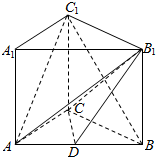 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AC=4,BC=3,AB=5,AA1=4,点D是AB的中点.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AC=4,BC=3,AB=5,AA1=4,点D是AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 运费(元/吨) | ||
| 甲库 | 乙库 | |
| A镇 | 240+10a | 180 |
| B镇 | 260 | 210 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$f(2)<4f($\sqrt{2}$) | B. | $\sqrt{2}$f(2)>4f($\sqrt{2}$) | ||
| C. | $\sqrt{2}$f(2)=4f($\sqrt{2}$) | D. | 两者大小关系无法确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 40小时 | B. | 50小时 | C. | 60小时 | D. | 80小时 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com