
| 运费(元/吨) | ||
| 甲库 | 乙库 | |
| A镇 | 240+10a | 180 |
| B镇 | 260 | 210 |
分析 列出线性约束条件,目标函数,作出可行域,求出最值,可得结论.
解答 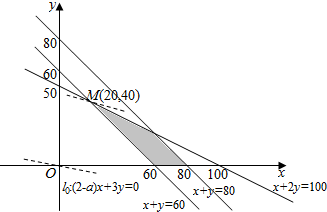 解:设甲、乙库往A镇运送x、y 吨大米,则甲、乙库往B镇运送100-x、80-y吨大米.
解:设甲、乙库往A镇运送x、y 吨大米,则甲、乙库往B镇运送100-x、80-y吨大米.
依题意有:$\left\{\begin{array}{l}{x+y≥60}\\{(100-x)+(80-y)≥100}\\{100-x≥2y}\\{x,y≥0}\end{array}\right.$,整理得:$\left\{\begin{array}{l}{60≤x+y≤80}\\{x+2y≤100}\\{x,y≥0}\end{array}\right.$,
根据上述约束条件作出可行域,如下图所示:
设总运费为z,则z=(240+10a)x+260(100-x)+180y+210(80-y)=(10a-20)x-30y+42800
目标直线为l:y=$\frac{a-2}{3}$x+$\frac{4280}{3}$-$\frac{z}{30}$,
且l越上移z的值越小,因为$\frac{1}{2}$<a<2,所以斜率$\frac{a-2}{3}$∈(-$\frac{1}{2}$,0),
如图,当l过点M(20,40)时,Z的值取得最小,
答:应该按甲库往A镇运送的大米量为20吨;乙库往A镇运送的大米量为40吨的方案派送大米,总运费最省.
点评 本题考查线性规划知识的运用,考查利用数学知识解决实际问题,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-e-2) | B. | (-1-e-2,-e-2) | C. | (-1-e-2,0) | D. | (-1-e-2,-1-3e-4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∨¬q | B. | ¬p∧q | C. | ¬q∧¬q | D. | p∧q |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{1}{2}$ | C. | ±$\frac{1}{2}$ | D. | ±2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,2] | B. | [-1,2] | C. | (-∞,-1)∪(2,+∞) | D. | (-∞,-1]∪(2,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com