练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    18．若-1＜x＜1，-1＜y＜1，求证：$（\frac{x-y}{1-xy}）^{2}$＜1．

    分析 通过题意，利用分析法可知要证$（\frac{x-y}{1-xy}）^{2}$＜1，即证|x-y|＜|1-xy|，两边平方后即证（1-x2）（1-y2）＞0，进而可得结论．

    解答 证明：∵-1＜x＜1，-1＜y＜1，
    ∴|1-xy|＞0，|x-y|≥0，
    要证$（\frac{x-y}{1-xy}）^{2}$＜1，只要证|$\frac{x-y}{1-xy}$|＜1，即证|x-y|＜|1-xy|，
    只要证（x-y）2＜（1-xy）2，即证（1-x2）（1-y2）＞0，
    而由|x|＜1，|y|＜1可得（1-x2）（1-y2）＞0成立，
    故原不等式成立．

    点评 本题考查不等式的证明，考查运算求解能力，注意解题方法的积累，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    8．过M（1，2$\sqrt{2}$）作直线与抛物线y2=8x，有且只有一个公共点，这样的直线有（　　）条．
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．设函数f（x）=sin（ωx+φ）+cos（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）的最小正周期为π，当x=$\frac{π}{12}$时，f（x）取得最大值．
    （1）求f（x）的解析式；
    （2）求出f（x）的单调区间．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．等比数列{an}中各项均为正数a1a5=4，a4=1，则{an}的公比q为（　　）
    A．2B．$\frac{1}{2}$C．±$\frac{1}{2}$D．±2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．己知等差数列{an}中，a2=2，a5=5．
    （Ⅰ）若bn=2${\;}^{{a}_{n}}$，求数列{bn}的前n项的和Sn
     （Ⅱ）若c1=a1，cn-cn-1=an，求数列{cn}的通项公式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．已知三棱锥P-ABC的四个顶点在半径为2的球面上，且PA⊥平面ABC，若AB=2，AC=$\sqrt{3}$∠BAC=$\frac{π}{2}$，则三棱锥P-ABC的体积是$\sqrt{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知等差数列{an}的首项为1，前n项和为Sn，且S1，S3，S9成等比数列．
    （Ⅰ）求数列{an}的通项公式；
    （Ⅱ）记Tn为数列{$\frac{1}{{a}_{n+1}{a}_{n}}$}的前n项和，求Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

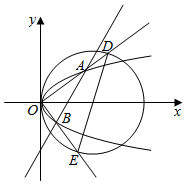    7．如图所示，过点（1，0）的直线与抛物线y2=x交于A、B两点，射线OA和OB分别和圆（x-2）2+y2=4交于D、E两点，若$\frac{{S}_{△OAB}}{{S}_{△ODE}}$=λ，则λ的最小值是（　　）
    A．$\frac{1}{2}$B．$\frac{1}{3}$C．$\frac{1}{4}$D．$\frac{1}{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

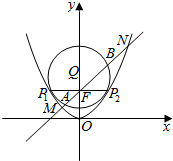    8．如图，抛物线C：x2=2py（p＞0）的焦点为F（0，1），取垂直于y轴的直线与抛物线交于不同的两点P1，P2．过P1，P2作圆心为Q的圆，使抛物线的其余点均在圆外，且P1Q⊥P2Q．
    （1）求抛物线C和圆Q的方程；
    （2）过点F作直线，与抛物线C和圆Q依次交于M，A，B，N，求|MN|•|AB|的最小值．

    查看答案和解析>>

    同步练习册答案