
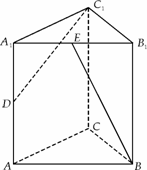
如右图,在正三棱柱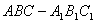 中,
中,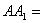
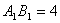 ,
,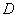 、
、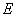 分别为
分别为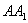 与
与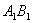 的中点.
的中点.
(1)求异面直线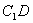 与
与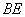 的夹角;
的夹角;
(2)求四面体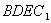 体积.
体积.
 学业测评一课一测系列答案
学业测评一课一测系列答案科目:高中数学 来源: 题型:
直线ax+by+c=0同时要经过第一、第二、第四象限,则a,b,c应满足( )
A.ab>0,bc<0 B.ab>0,bc>0
C.ab<0,bc>0 D.ab<0,bc<0
查看答案和解析>>
科目:高中数学 来源: 题型:
在古希腊,毕达哥拉斯学派把1,3,6,10,15,……这些数叫做三角形数,因为这些数目的石 子可以排成一个正三角形(如下图)

则第八个三角形数是 ( )
A. 35 B. 36 C. 37 D. 38
查看答案和解析>>
科目:高中数学 来源: 题型:
若二次函数f(x)=ax2+bx+c(a≠0)满足f(x+1)-f(x)=2x,且f(0)=1.
(1)求f(x)的解析式;
(2)若在区间[-1,1]上,不等式f(x)>2x+m恒成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com