
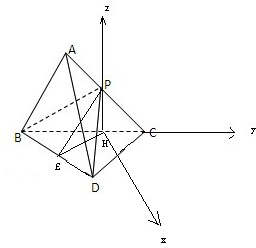
 已知△ABC和△DBC是两个有公共斜边的直角三角形,并且AB=AD=AC=2a,CD=
已知△ABC和△DBC是两个有公共斜边的直角三角形,并且AB=AD=AC=2a,CD=| 6 |
6
| ||
| 7 |
| BC |
| 2 |
| n |
| 3 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 3 |
| 6 |
| 2 |
| ||
| 2 |
| 2 |
| 6 |
| ||
| 2 |
x2+(
|
|
| ||
| 2 |
|
| 2 |
6
| ||
| 7 |
6
| ||
| 7 |
8
| ||
| 7 |
6
| ||
| 7 |
| ||
| 2 |
| 9 |
| 14 |
| 2 |
| PB |
| 8 |
| 7 |
| 2 |
| 6 |
| 7 |
| 2 |
| PC |
6
| ||
| 7 |
6
| ||
| 7 |
| PD |
| ||
| 2 |
| 9 |
| 14 |
| 2 |
| 6 |
| 7 |
| 2 |
| m |
| m |
| PC |
| m |
| PD |
|
| m |
| 3 |
| n |
| n |
| PB |
| n |
| PD |
|
| n |
| 3 |
| n |
| m |
| 3-3+4 | ||||
|
2
| ||
| 35 |
| ||
| 2 |
| ||
| 2 |
| BC |
| 2 |
| n |
| 3 |
|
| ||||
|
|
|0-6
| ||
|
3
| ||
| 7 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 3 |
| 3 |
| 3 |


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
 如图,已知△ABC的面积为14,D、E分别为边AB、BC上的点,且AD:DB=BE:EC=2:1,AE与CD交于P.设存在λ和μ使
如图,已知△ABC的面积为14,D、E分别为边AB、BC上的点,且AD:DB=BE:EC=2:1,AE与CD交于P.设存在λ和μ使| AP |
| AE |
| PD |
| CD |
| AB |
| a |
| BC |
| b |
| a |
| b |
| BP |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在四棱锥S-ABCD中,SA⊥底面ABCD,∠BAD=∠ABC=90°,BC=3SA=3AB=3AD.
如图,在四棱锥S-ABCD中,SA⊥底面ABCD,∠BAD=∠ABC=90°,BC=3SA=3AB=3AD.查看答案和解析>>
科目:高中数学 来源: 题型:
 A、已知:如图,在△ABC中,∠ABC=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,连接DB、DE、OC.若AD=2,AE=1,求CD的长.
A、已知:如图,在△ABC中,∠ABC=90°,O是AB上一点,以O为圆心,OB为半径的圆与AB交于点E,与AC切于点D,连接DB、DE、OC.若AD=2,AE=1,求CD的长.| 1 |
| 1 |
| 1 |
| 1×2 |
| 1 |
| 1×2×3 |
| 1 |
| 1×2×3×L×n |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
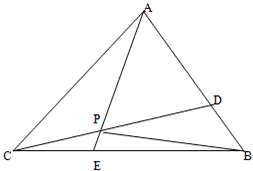 如图,已知△ABC的面积为14,D、E分别为边AB、BC上的点,且AD:DB=BE:EC=2:1,AE与CD交于P.设存在λ和μ使
如图,已知△ABC的面积为14,D、E分别为边AB、BC上的点,且AD:DB=BE:EC=2:1,AE与CD交于P.设存在λ和μ使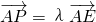 ,
,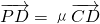 ,
,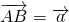 ,
,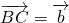 .
. ,
, 表示
表示 ;
;查看答案和解析>>
科目:高中数学 来源:2008-2009学年江苏省南通市启东中学高三(下)5月月考数学试卷(解析版) 题型:解答题
 +
+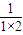 +
+ +L+
+L+ <2.
<2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com