
分析 利用△F1PF2的重心为G,内心为I,结合三角形的面积公式,直线y=x+$\sqrt{6}$与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,求出几何量,即可求出椭圆的方程;设直线l为y=k(x-1),直线l和椭圆交于M(x1,y1),N(x2,y2).将y=k(x-1)代入3x2+4y2=12中,得(3+4k2)x2-8k2x+4k2-12=0,由此利用韦达定理能求出直线MN的方程.
解答 解:设P(x0,y0)(y0≠0),F1(-c,0),F2(c,0),
则G($\frac{{x}_{0}}{3}$,$\frac{{y}_{0}}{3}$),
设I(xI,yI),∵IG∥F1F2,∴yI=$\frac{{y}_{0}}{3}$,
∵|F1F2|=2c,∴${S}_{△{F}_{1}P{F}_{2}}$=$\frac{1}{2}$|F1F2||y0|=$\frac{1}{2}$(|PF1|+|PF2|+|F1F2|)•$\frac{{y}_{0}}{3}$,
∴2c•3=2a+2c,即a=2c,
∵直线y=x+$\sqrt{6}$与以原点为圆心,以椭圆C的短半轴长为半径的圆相切,
∴b=$\frac{\sqrt{6}}{\sqrt{2}}$=$\sqrt{3}$,∴a2-c2=3,
解得a=2,c=1,
∴椭圆的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,
若直线l斜率不存在,显然k1+k2=0不合题意;
则直线l的斜率存在.设直线l为y=k(x-1),
直线l和椭圆交于M(x1,y1),N(x2,y2).
将y=k(x-1)代入3x2+4y2=12中,得:
(3+4k2)x2-8k2x+4k2-12=0,
依题意:△=9k2+9>0,
由韦达定理知:$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=\frac{8{k}^{2}}{3+4{k}^{2}}}\\{{x}_{1}{x}_{2}=\frac{4{k}^{2}-12}{3+4{k}^{2}}}\end{array}\right.$,
又kAM+kAN=$\frac{{y}_{1}}{{x}_{1}+2}$+$\frac{{y}_{2}}{{x}_{2}+2}$=k($\frac{{x}_{1}-1}{{x}_{1}+2}$+$\frac{{x}_{2}-1}{{x}_{2}+2}$)
=k[2-3($\frac{1}{{x}_{1}+2}$+$\frac{1}{{x}_{2}+2}$)],
$\frac{1}{{x}_{1}+2}$+$\frac{1}{{x}_{2}+2}$=$\frac{{x}_{1}+{x}_{2}+4}{{x}_{1}{x}_{2}+2({x}_{1}+{x}_{2})+4}$
=$\frac{8{k}^{2}+4(3+4{k}^{2})}{4{k}^{2}-12+16{k}^{2}+4(3+4{k}^{2})}$
=$\frac{1+2{k}^{2}}{3{k}^{2}}$,
从而kAM+kAN=k(2-3•$\frac{1+2{k}^{2}}{3{k}^{2}}$)=-$\frac{1}{k}$=-$\frac{1}{2}$,
解得k=2,符合△>0.
故所求直线MN的方程为:y=2(x-1).
故答案为:y=2x-2.
点评 本题考查椭圆方程,考查直线与椭圆,直线与圆的位置关系,考查韦达定理的运用,考查学生的计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | A⊆B | B. | B⊆A | ||
| C. | A∩B=∅ | D. | 集合A、B间没有包含关系 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{8\sqrt{3}}{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
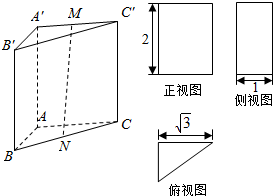 已知一个三棱柱ABC-A′B′C′的三视图由一个直角三角形和两个矩形组成,如图若M,N分别是A′C′,BC的中点.
已知一个三棱柱ABC-A′B′C′的三视图由一个直角三角形和两个矩形组成,如图若M,N分别是A′C′,BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com