
【题目】设实数x,y满足约束条件 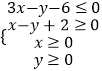 ,若目标函数z=ax+by(a>0,b>0)的最大值为10,则a2+b2的最小值为 .
,若目标函数z=ax+by(a>0,b>0)的最大值为10,则a2+b2的最小值为 .
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:
【题目】甲乙两个学校高三年级分别有1100人,1000人,为了了解两个学校全体高三年级学生在该地区二模考试的数学成绩清况,采用分层抽样方法从两个学校一共抽取了105名学生的数学成绩,并作出了频数分布统计表如下:
甲校:
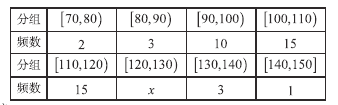
乙校:
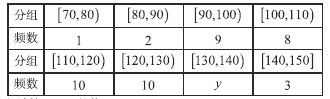
(1)计算![]() 的值;
的值;
(2)若规定考试成绩在![]() 内为优秀,请根据样本估计乙校数学成绩的优秀率;
内为优秀,请根据样本估计乙校数学成绩的优秀率;
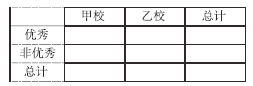
(3)由以上统计数据填写下面![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为两个学校的数学成绩有差异.
的把握认为两个学校的数学成绩有差异.

附: 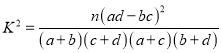 ;
; ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:x1 , x2是方程x2﹣mx﹣1=0的两个实根,且不等式a2+4a﹣3≤|x1﹣x2|对任意m∈R恒成立;命题q:不等式x2+2x+a<0有解,若命题p∨q为真,p∧q为假,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cos
=(cos ![]() x,sin
x,sin ![]() x),
x), ![]() =(cos
=(cos ![]() ,﹣sin
,﹣sin ![]() ),且x∈[﹣
),且x∈[﹣ ![]() ,
, ![]() ]
]
(1)求 ![]()
![]() 及|
及| ![]() +
+ ![]() |;
|;
(2)若f(x)= ![]()
![]() ﹣|
﹣| ![]() +
+ ![]() |,求f(x)的最大值和最小值.
|,求f(x)的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,若A,B,C成等差数列,2a,2b,2c成等比数列,则cosAcosB=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015男篮亚锦赛决赛阶段,中国男篮以![]() 连胜的不败成绩赢得第
连胜的不败成绩赢得第![]() 届亚锦赛冠军,同时拿到亚洲唯一
届亚锦赛冠军,同时拿到亚洲唯一![]() 张直通里约奥运会的入场券.赛后,中国男篮主力易建联荣膺本届亚锦赛
张直通里约奥运会的入场券.赛后,中国男篮主力易建联荣膺本届亚锦赛![]() (最有价值球员),下表是易建联在这
(最有价值球员),下表是易建联在这![]() 场比赛中投篮的统计数据.
场比赛中投篮的统计数据.
比分 | 易建联技术统计 | |||
投篮命中 | 罚球命中 | 全场得分 | 真实得分率 | |
中国 |
|
|
|
|
中国 |
|
|
|
|
中国 |
|
|
|
|
中国 |
|
|
|
|
中国 |
|
|
|
|
中国 |
|
|
|
|
中国 |
|
|
|
|
中国 |
|
|
|
|
中国 |
|
|
|
|
注:(1)表中![]() 表示出手
表示出手![]() 次命中
次命中![]() 次;
次;
(2)![]() (真实得分率)是衡量球员进攻的效率,其计算公式为:
(真实得分率)是衡量球员进攻的效率,其计算公式为:
![]()
(1)从上述![]() 场比赛中随机选择一场,求易建联在该场比赛中
场比赛中随机选择一场,求易建联在该场比赛中![]() 超过
超过![]() 的概率;
的概率;
(2)我们把比分分差不超过![]() 分的比赛称为“胶着比赛”.为了考验求易建联在“胶着比赛”中的发挥情况,从“胶着比赛”中随机选择两场,求易建联在这两场比赛中
分的比赛称为“胶着比赛”.为了考验求易建联在“胶着比赛”中的发挥情况,从“胶着比赛”中随机选择两场,求易建联在这两场比赛中![]() 至少有一场超过
至少有一场超过![]() 的概率;
的概率;
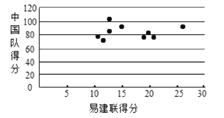
(3)用![]() 来表示易建联某场的得分,用
来表示易建联某场的得分,用![]() 来表示中国队该场的总分,画出散点图如图所示,请根据散点图判断
来表示中国队该场的总分,画出散点图如图所示,请根据散点图判断![]() 与
与![]() 之间是否具有线性相关关系?结合实际简单说明理由.
之间是否具有线性相关关系?结合实际简单说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=sinx的图象上所有的点向右平行移动 ![]() 个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是( )
个单位长度,再把所得各点的横坐标伸长到原来的2倍(纵坐标不变),所得图象的函数解析式是( )
A.y=sin(2x﹣ ![]() )
)
B.y=sin(2x+ ![]() )
)
C.y=sin( ![]() x﹣
x﹣ ![]() )
)
D.y=sin( ![]() x﹣
x﹣ ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD,侧面PAD是边长为2的正三角形,且与底面垂直,底面ABCD是∠ABC=60°的菱形,M为PC的中点.
(Ⅰ) 求证:PC⊥AD;
(Ⅱ) 在棱PB上是否存在一点Q,使得A,Q,M,D四点共面?若存在,指出点Q的位置并证明;若不存在,请说明理由;
(Ⅲ) 求点D到平面PAM的距离. 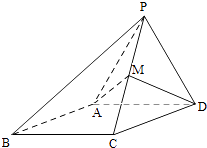
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com