
【题目】已知命题p:x1 , x2是方程x2﹣mx﹣1=0的两个实根,且不等式a2+4a﹣3≤|x1﹣x2|对任意m∈R恒成立;命题q:不等式x2+2x+a<0有解,若命题p∨q为真,p∧q为假,求a的取值范围.
【答案】解:命题p:x1 , x2是方程x2﹣mx﹣1=0的两个实根,∴△=m2+4≥0.x1+x2=m,x1x2=﹣1.
∴|x1﹣x2|= ![]() =
= ![]() .
.
∵不等式a2+4a﹣3≤|x1﹣x2|对任意m∈R恒成立,∴a2+4a﹣3≤2,解得﹣5≤a≤1;
命题q:不等式x2+2x+a<0有解,∴△=4﹣4a>0,解得a<1.
∵命题p∨q为真,p∧q为假,
∴p与q必然一真一假,
∴ ![]() ,或
,或 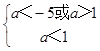 ,
,
解得a=1,或a<﹣5.
∴a的取值范围是a=1或a<﹣5
【解析】命题p:x1 , x2是方程x2﹣mx﹣1=0的两个实根,可得△≥0.利用根与系数的关系|x1﹣x2|= ![]() =
= ![]() .即可得出最小值.不等式a2+4a﹣3≤|x1﹣x2|对任意m∈R恒成立,解得a范围;命题q:不等式x2+2x+a<0有解,可得△>0,解得a范围.由于命题p∨q为真,p∧q为假,可得p与q必然一真一假,即可得出.
.即可得出最小值.不等式a2+4a﹣3≤|x1﹣x2|对任意m∈R恒成立,解得a范围;命题q:不等式x2+2x+a<0有解,可得△>0,解得a范围.由于命题p∨q为真,p∧q为假,可得p与q必然一真一假,即可得出.
【考点精析】本题主要考查了复合命题的真假的相关知识点,需要掌握“或”、 “且”、 “非”的真值判断:“非p”形式复合命题的真假与F的真假相反;“p且q”形式复合命题当P与q同为真时为真,其他情况时为假;“p或q”形式复合命题当p与q同为假时为假,其他情况时为真才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点.从A点测得 M点的仰角∠MAN=60°,C点的仰角∠CAB=45°以及∠MAC=75°;从C点测得∠MCA=60°.已知山高BC=100m,则山高MN=m. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin(x﹣ ![]() )(x∈R),下面结论错误的是( )
)(x∈R),下面结论错误的是( )
A.函数f(x)的最小正周期为2π
B.函数f(x)在区间[0, ![]() ]上是增函数
]上是增函数
C.函数f(x)的图象关于直线x=0对称
D.函数f(x)是奇函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校有教职工500人,对他们进行年龄状况和受教育程度的调查,其结果如下:
高中 | 专科 | 本科 | 研究生 | 合计 | |
35岁以下 | 10 | 150 | 50 | 35 | 245 |
35﹣50 | 20 | 100 | 20 | 13 | 153 |
50岁以上 | 30 | 60 | 10 | 2 | 102 |
随机的抽取一人,求下列事件的概率:
(1)50岁以上具有专科或专科以上学历;
(2)具有本科学历;
(3)不具有研究生学历.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,cos2B﹣5cos(A+C)=2.
(1)求角B的值;
(2)若cosA= ![]() ,△ABC的面积为10
,△ABC的面积为10 ![]() ,求BC边上的中线长.
,求BC边上的中线长. 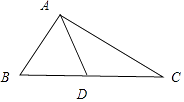
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若一个四位数的各位数字相加和为![]() ,则称该数为“完美四位数”,如数字“
,则称该数为“完美四位数”,如数字“![]() ”.试问用数字
”.试问用数字![]() 组成的无重复数字且大于
组成的无重复数字且大于![]() 的“完美四位数”有( )个
的“完美四位数”有( )个
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设向量 ![]() =(
=( ![]() sinx,sinx),
sinx,sinx), ![]() =(cosx,sinx),x∈[0,
=(cosx,sinx),x∈[0, ![]() ].
].
(1)若| ![]() |=|
|=| ![]() |,求x的值;
|,求x的值;
(2)设函数f(x)= ![]()
![]() ,求f(x)的最大值及单调递增区间.
,求f(x)的最大值及单调递增区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com