Question

【题目】在△ABC中，角A，B，C所对的边分别为a，b，c，cos2B﹣5cos（A+C）=2．
（1）求角B的值；
（2）若cosA= ，△ABC的面积为10 ，求BC边上的中线长．

Answer 1

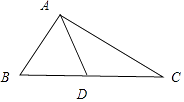
【答案】
（1）解：∵cos2B﹣5cos（A+C）=2．

∴2cos2B+5cosB﹣3=0，解得：cosB= 或﹣3（舍去），又B∈（0，π），

∴B=

（2）解：∵cosA= ，∴可得：sinA= ，

∴sinC=sin（A+B）=sinAcosB+cosAsinB= × + × = ，

∴ = ，

设b=7x，c=5x，则在△ABC中，由余弦定理得BC2=AB2+AC2﹣2ABACcosA，

∴BC= =8x，

∵△ABC的面积为10 = ABBCsinB= ×5x×8x× ，解得：x=1，

∴AB=5，BC=8，AC=7，BD=4，

∴在△ABD中，由余弦定理得AD2=AB2+BD2﹣2ABBDcosB=25+16﹣2×5×4× =21，

∴解得：AD= ．

【解析】（1）利用三角函数恒等变换的应用化简已知等式可得2cos2B+5cosB﹣3=0，进而解得cosB，结合B的范围即可得解B的值；（2）先根据两角和差的正弦公式求出sinC，再根据正弦定理得到b，c的关系，再利用余弦定理可求BC的值，再由三角形面积公式可求AB，BD的值，利用余弦定理即可得解AD的值．
【考点精析】掌握正弦定理的定义是解答本题的根本，需要知道正弦定理:．